Distribuição normal, um método estatístico comumente utilizado na área de dados e no dia a dia de uma pessoa que trabalha com estatística. Provavelmente você já deve ter ouvido falar sobre essa distribuição.
A compreensão sobre esse tipo de distribuição nem sempre é fácil, dada a densa trajetória matemática cobrada para entender e resolver problemas do tipo. Pensando nisso, elaboramos um material que vai auxiliar você a entender de maneira didática como funciona essa distribuição e suas aplicações.
Nesse post você verá sobre:
- O que é distribuição normal?
- Como saber se a distribuição é normal?
- Como criar uma curva de distribuição normal no R?
- Como ler a curva da distribuição normal?
- Entenda a função densidade de probabilidade normal
- Entenda a função de distribuição acumulada normal
- Qual a relação entre a distribuição normal e o Teorema do Limite Central?
- Quais os tipos de distribuição estatística discreta?
- Exercício de distribuição normal resolvido!
O que é distribuição normal?
A distribuição normal ou distribuição gaussiana é considerada uma das distribuições mais importantes da estatística, famosa também pelo seu formato de sino. Para defini-la, primeiro precisamos entender o que é um evento aleatório. Para exemplo disso, o lançamento de um dado e de uma moeda são eventos aleatórios. No caso dos dados, é possível obter seis resultados distintos (1,2,3,4,5,6) e para a moeda, dois (cara ou coroa).
Logo, entendemos por evento aleatório os possíveis fenômenos que podem ser repetidos inúmeras vezes e obtém resultados imprevisíveis. Mas, apesar de serem eventos imprevisíveis, podemos extrair algumas conclusões, pois muitos apresentam padrões de comportamentos quando repetidos inúmeras vezes.
Esses eventos aleatórios que seguem padrão são chamados de distribuição normal, sendo definida como uma variável aleatória contínua, ou seja, uma variável que pode assumir infinitos valores. Ela pode apresentar diversos processos práticos, como altura ou peso de um grupo de pessoas, a pressão sanguínea de uma população, o tempo que um grupo de pessoas usa na realização de provas. É importante destacar que nessa distribuição, a média, a mediana e a moda possuem o mesmo valor.
Como saber se a distribuição é normal?
A função densidade de probabilidade de uma distribuição normal é dada pela seguinte equação:
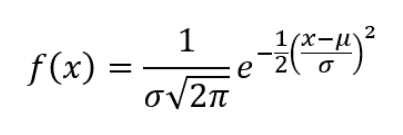
Para nos referirmos a ela, usamos a seguinte notação:
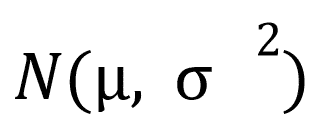
Para executar esse cálculo, é importante ter em mente que ele não possui solução analítica, ou seja, o cálculo precisa ser realizado por meio de um método numérico. Para isso, é necessário integrar a função f(x), resolvendo os limites de integração da faixa de valores desejada.
Como criar uma curva de distribuição normal no R?
Para falarmos sobre tal curva, ou o famoso sino, vamos gerar número aleatórios no R em distribuição normal e plotar o nosso gráfico. Nesse exemplo, queremos 1000 números em uma distribuição normal com média igual a 2 e desvio padrão (sd) igual a 1.
Por meio do comando, geramos a distribuição:
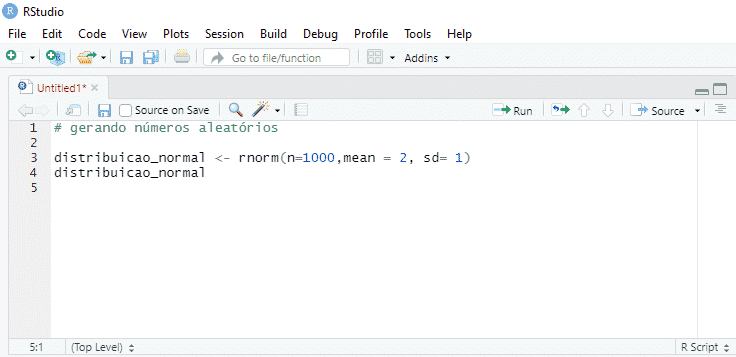
Para plotar o nosso histograma executamos o seguinte comando:
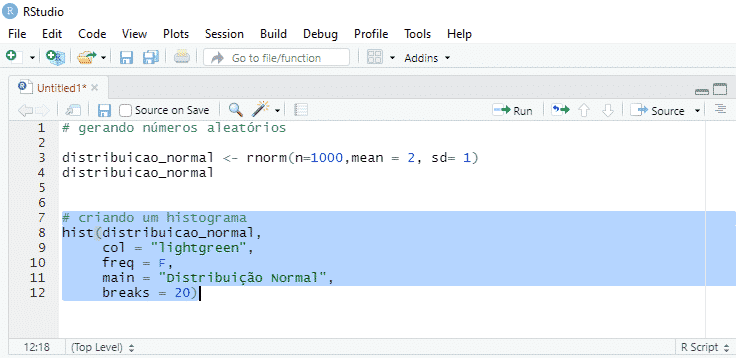
Em que obtemos o seguinte gráfico:
Agora, vamos desenhar a curva no gráfico:
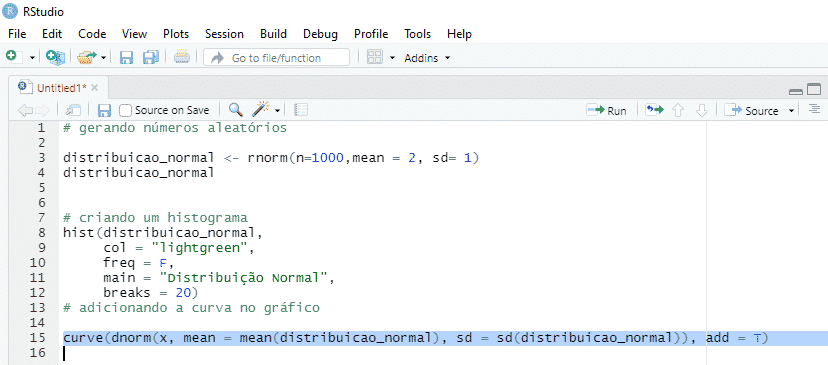
Aqui obtemos o nosso gráfico final:
Como ler a curva da distribuição normal?
Como pudemos observar, o gráfico de distribuição normal segue o padrão de uma curva, como destacado na figura abaixo (vamos usar o mesmo exemplo da figura anterior):
Logo, sempre que vermos a curva com esse formato, podemos afirmar que é uma variável aleatória contínua com distribuição normal.
Note também que esse formato segue uma simetria em relação ao centro dele. Assim, quando nos referimos ao valor central, estamos tratando da média. Os demais valores que se afastam da média nos ajudam a medir a dispersão dos dados, chamado de variância. Dessa forma, podemos afirmar que quanto maior for a curva, mais dispersos estão os dados em torno da média.
Entenda a função densidade de probabilidade normal
A função densidade de probabilidade normal é definida pela seguinte equação:
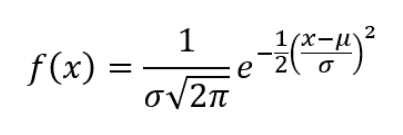
Na qual 
representa a média e 
, o desvio padrão, uma vez que auxiliam na definição de onde está centralizada (média) e o seu grau de dispersão. Nesse sentido, vale destacar que assim como em outros modelos, existem diferentes distribuições normais, a depender dos parâmetros. Lembrando que essa função densidade de probabilidade normal também é conhecida como gaussiana.
A função densidade de probabilidade normal é calculada por meio de método numérico ou outras formas de aproximação.
Entenda a função de distribuição acumulada normal
A função de distribuição acumulada é responsável por calcular a probabilidade acumulada para um determinado valor. A exemplo disso, podemos determinar a probabilidade de observações aleatórias.
Qual a relação entre a distribuição normal e o Teorema do Limite Central?
O Teorema Central do Limite é responsável por detalhar a maneira de distribuição da média, visto que esse teorema é fundamental na descrição de estatísticas e probabilidades. À exemplo disso, quando estamos tratando de tamanhos amostrais grandes, a distribuição da média define uma distribuição normal.
Quais os tipos de distribuição estatística discreta?
Distribuição de Poisson
Primeiro, vamos definir eventos que podem ser calculados por meio da distribuição normal, uma vez que esta distribuição está relacionada a “eventos raros”, como acidentes de carro, chegada de clientes em um banco, etc.
A distribuição de Poisson é utilizada quando o número de eventos discretos é maior que o número médio de eventos em um determinado intervalo de tempo ou espaço. Nesse sentido, o número de ocorrências/eventos não necessariamente está definido, uma vez que os resultados ocorrem de forma aleatória, sendo os eventos independentes.
Distribuição Binomial
Quando tratamos de experimentos com repetição, como por exemplo o lançamento de uma moeda em que os possíveis resultados são cara ou coroa, ou seja, sucesso ou fracasso, estamos tratando de eventos de uma distribuição binomial. Nesse sentido, a probabilidade de cada resultado pode ser encontrada por meio de um diagrama de árvore ou regra da multiplicação, mas para isso temos também uma equação generalizada.
Exercício de distribuição normal resolvido!
Para exemplificar de modo didático, vamos resolver um exemplo generalizado aplicando a distribuição normal no software R.
Seja uma variável aleatória com distribuição N(100,100), calcule as seguintes probabilidades:
- P[X<90]
- P[90<X<110]
- P[X>90]
No R, utilizamos o comando pnorm para calcular a probabilidade:
> pnorm(90, 100, 10)
[1] 0.1586553
> pnorm(110, 100, 10) - pnorm(90, 100, 10)
[1] 0.6826895
> 1 - pnorm(90, 100, 10)
[1] 0.8413447
Viu? É só plotar os comandos com os parâmetros adequados que você encontrará os resultados da sua distribuição normal!
Espero que agora isso seja um assunto compreensível para você. Ela é uma das distribuições estatísticas mais importantes e as suas aplicações são importantes para eventuais manipulações com dados.
Agora, tente resolver problemas com os softwares utilizados no artigo e replique alguns códigos para fixar melhor o aprendizado.
Não esqueça de ver a nossa trilha de aprendizagem sobre Excel que também é uma ferramenta bastante útil no dia a dia para trabalhar com dados.
