É fato afirmar que a estatística está presente no dia a dia de grande parte das pessoas. Em meados de 2021, com a pandemia COVID-19, foram necessárias várias análises estatísticas por cientistas para verificar os casos diários, se os casos aumentavam ou diminuíam com o passar dos dias, semanas, etc. 

Contudo, nessas análises feitas, há uma grande quantidade de cálculos realizados nelas. E, isso pode ser motivo de medo para pessoas que desejam trabalhar com estatística, pois é uma área que trabalha o tempo todo com operações matemáticas. Não ter uma boa base dessa matéria tornará o aprendizado dessa área muito difícil. 

Se você gosta de fazer gráficos, comparar dados, extrair informações de um determinado conjunto de dados, a estatística pode abrir várias portas para quem possui esse perfil. Caso você não entenda muito bem, não se preocupe, pois exploraremos a fundo os principais conceitos de estatística neste artigo. 

• O que é estatística?
• Para que serve a estatística?
• Quais os 2 tipos de estatística?
• Quais as 7 etapas do método estatístico?
• Quais os princípios da estatística?
• Sistemas lineares: o que são e quais os tipos?
• Média, moda e mediana: conheça as medidas de tendência central!
• Amplitude, desvio, variância e desvio padrão: conheça as medidas de dispersão!
• 5 exercícios de estatística resolvidos!
• Como é o curso de estatística?
• Como está o mercado de trabalho para um profissional formado em estatística?

Preparado(a)? Vamos lá! 

O que é estatística?

A estatística é o estudo da coleta, análise, interpretação e organização dos dados de uma forma específica. Para que essa análise seja feita, são utilizadas algumas técnicas da matemática, tais como álgebra linear, equações diferenciais e probabilidade de eventos. 

Quando duas equipes vão jogar uma partida de futebol, pessoas estatísticas fazem uma análise de qual as chances cada equipe terá de vencer a partir de muitos fatores, como retrospecto, pontuação, etc. Ou seja, a estatística seria como se fosse um raio-x que fazemos de alguma situação, mas o resultado seria numérico, neste caso.

Muitas pessoas pesquisadoras precisam tomar decisões com base em dados estatísticos, fazer sua própria interpretação depois de uma análise de dados feita, enfim, para pessoas que trabalhem com esse segmento, basicamente farão cálculos e análises a cada dia.

 Para que serve a estatística?

A estatística serve para termos uma análise de dados de um determinado evento, para termos uma noção geral do que está ocorrendo nele. Um exemplo disso seria o caso da pandemia COVID-19, pois todo o mundo precisou e ainda precisa de pessoas que trabalham com estatística para realizar pesquisas com relação ao vírus. 

Além disso, para saber a propagação do vírus, gráficos e levantamentos diários foram feitos para ver como o vírus se propagava e, qual o número de óbitos por dia, se ele aumentava ou diminuía. Assim, pessoas que trabalhem com análise de dados na estatística, tiveram uma grande carga de trabalho para essa pandemia, que alastrou o mundo.

Desse modo, não basta simplesmente coletar um dado e analisar ele. Há alguns procedimentos para serem feitos para coleta de dados e para sua posterior análise e, essas regras são desenvolvidas com base no estudo da estatística. 

 Quais os 2 tipos de estatística?

Vejamos agora os dois tipos de estatística que existem:

Estatística descritiva

Na estatística descritiva, os dados são exibidos de forma resumida, sem a necessidade deles serem generalizados. Para isso, há o uso de tabelas e gráficos, representando um conjunto de dados. 

Estatística inferencial

Na estatística inferencial, fazemos uma generalização com base no que foi coletado na estatística descritiva. Nesse tipo, podemos tirar conclusões e formular hipóteses de algum evento que ocorreu. 

Por exemplo, se em um concurso foram inscritos 100 pessoas e 60% dos inscritos for do sexo feminino, poderemos inferir que o alvo do concurso foram mulheres. 

 Quais as 7 etapas do método estatístico?

 As etapas para podermos fazer uma análise de dados de forma nítida são as seguintes: 

1. Definirmos o problema: especificar qual problema nossa análise de dados procura resolver;
2. Planejamento: elaborarmos métodos para podermos analisar os dados da melhor forma possível;
3. Coleta de dados: após fazermos as duas etapas acima, coletamos os dados para podermos dar início em nossa análise;
4. Correção dos dados coletados: realizar uma conferência dos dados para ter certeza que eles não apresentam nenhum erro;
5. Apuração dos dados: será feita a organização e a ordenação dos dados da forma desejada;
6. Apresentação dos dados: será montada uma estrutura que demonstra os resultados da coleta de dados, podendo ser gráficos ou tabelas;
7. Análise dos dados: podemos, então, fazer conclusões e formular hipóteses, com os dados sendo analisados. 

A seguir, veremos alguns dos princípios básicos mais importantes para o estudo da estatística.

 Quais os princípios da estatística?

População/universo estatístico

A população seria o conjunto dos elementos que estamos analisando. Eles podem ser números, objetos, pessoas, etc. 

Exemplo de população/universo estatístico

Um exemplo de população seria avaliar qual a marca de suco em caixa que as pessoas mais compram nos supermercados. Ou seja, a população nesse caso seria todas as marcas de sucos que vêm em caixa nos supermercados. 

Dado estatístico

Dados estatísticos seriam os valores obtidos quando uma análise estatística é realizada. A partir deles, conseguimos formular hipóteses ou conclusões. 

Exemplo de dado estatístico

Um exemplo seria quando uma pessoa utiliza uma moeda e joga ela ao ar dez vezes, anotando o resultado, se é cara ou coroa. Fazendo isso, os resultados são os seguintes: 

Lançamento	Resultado
1	cara
2	cara
3	cara
4	coroa
5	coroa
6	cara
7	coroa
8	coroa
9	cara
10	coroa

Nesse caso, conforme exibido na tabela acima, a coluna resultado seria a coluna que representa os dados estatísticos. 

Variável e os tipos de variáveis estatísticas

A seguir, verificaremos alguns tipos de variáveis existentes na estatística: 

Variáveis quantitativas

As variáveis quantitativas são variáveis que são “contáveis”, ou seja, podemos enumerar elas, pois seus valores são numéricos. Existem dois tipos de variáveis quantitativas: 

• Variável quantitativa contínua: quando o resultado é exibido em forma de intervalos, como, por exemplo: peso, altura, nível de glicose no sangue, pressão arterial, etc. 
• Variável quantitativa discreta: quando o resultado é finito, como, por exemplo, número de sobrinhos, pessoas em uma fila, etc. 

Variáveis qualitativas

As variáveis qualitativas são variáveis que não podemos enumerá-las, pois não são valores numéricos. Existem dois tipos de variáveis qualitativas: 

• Variável qualitativa ordinal: valores que possuem algum tipo de ordem ou grau atrelado a eles, como, por exemplo: graduação, pós-graduação, queimadura de 1º grau, 2º grau, 3º grau, etc. 
• Variável qualitativa nominal: valores que não possuem nenhuma ordem neles. Tais como: cor do cabelo, sexo, estado civil, cor dos olhos, etc. 

Amostra

Uma amostra seria a quantidade de pessoas entrevistadas em uma pesquisa. Ela também pode ser representada por uma coleta de uma quantidade pequena de algum item, como sal, açúcar ou água. Seu objetivo é que, com base nas amostras, conseguiremos tirar conclusões sobre o comportamento da população.  

Exemplo de amostra

Um exemplo seria fazer uma análise de um local em que há queixas de que a água está poluída. Para isso, não há a necessidade de coletar água de todo o local, basta coletarmos uma amostra, que seria somente uma quantidade pequena. 

Rol

Um rol seriam os dados dispostos para fazermos uma análise neles. Eles podem ser crescentes ou decrescentes. 

Exemplo de Rol

Uma pessoa possui dez primos e, a idade desses primos é: 22, 33, 34, 29, 51, 36, 12, 66, 14, 41. O rol seria justamente esses dados fornecidos para podermos, a partir de uma ordenação deles, fazer operações matemáticas. 

Nesse caso, o rol seria de idades desses primos e, ordenando ele de forma crescente, teremos: 12 ,14, 22, 29, 33, 34, 36, 41, 51, 66. 

Tabela de distribuição de frequência: absoluta, acumulada e relativa!

Tabela de distribuição de frequência absoluta

A frequência absoluta seria quantas vezes que um determinado número aparece em um conjunto.
Vamos utilizar o seguinte conjunto, de exemplo, com base em notas de alunos em um concurso, que seria nosso rol: 6, 6.5, 7, 7, 8.5, 7.5, 6, 7.5, 8.5, 9, 9, 7.

Para iniciarmos a tabela, pegamos sempre o menor valor do rol, que seria 6. Ao organizar nosso rol de forma crescente, ele ficará: 6, 6, 6.5, 7, 7, 7, 7.5, 7.5, 8.5, 8.5, 9, 9.

Nota	Frequência absoluta (quantas vezes o item aparece no rol)
6	2
6.5	1
7	3
7.5	2
8.5	2
9	2

Tabela de distribuição de frequência acumulada

Para construirmos a tabela de frequência acumulada, utilizaremos a de frequência absoluta anterior, como base. 

Nela, manteremos o primeiro item da frequência absoluta (que seria o 2) e, somaremos ele com o número da frequência absoluta da linha seguinte (que seria o 1). Isso terá que ser feito com cada linha da tabela: 

Nota	Frequência absoluta	Frequência acumulada
6	2	2
6.5	1	3 (2+1)
7	3	6 (3+3)
7.5	2	8 (6+2)
8.5	2	10 (8+2)
9	2	12 (10+2)

Ou seja, os números da frequência absoluta seriam: 2, 3, 6, 8, 10, 12, com base no exemplo. 

Tabela de distribuição de frequência relativa

Para a frequência relativa, também será utilizada a mesma tabela. Ela é calculada pela frequência absoluta, dividida pelo total de números do conjunto, multiplicado 100, para ficar em percentual. Vejamos a seguir:

Nota	Frequência absoluta	Frequência acumulada	Frequência relativa
6	2	2	2/12 x 100 = 16,67%
6.5	1	3 (2+1)	1/12 x 100 = 8,33%
7	3	6 (3+3)	3/12 x 100 = 25%
7.5	2	8 (6+2)	2/12 x 100 = 16,67%
8.5	2	10 (8+2)	2/12 x 100 = 16,67%
9	2	12 (10+2)	2/12 x 100 = 16,67%

Classes

Para distribuirmos frequência utilizando as classes, temos que organizar os dados que possuímos como rol em intervalos, na tabela de frequência. 

Exemplo de classes

Observando a tabela abaixo: 

Ela está representada por intervalos. Por exemplo, o (1,48 1,53], significa as pessoas que possuem altura entre 1.48cm e 1.53cm, assim como para o restante da tabela. 

Representação gráfica

Quais os principais tipos de gráficos?

Para podermos representar os dados feitos de forma evidente, utilizamos representações gráficas. Existem:

• Gráfico de ponto;
• Gráfico de barras;
• Gráfico de pizza;
• Gráfico de linhas;
• Gráfico de setor;
• Boxplot;
• Histograma.

Exemplo de representação gráfica

1. Gráfico de pontos:

2. Gráfico de barras:

3. Gráfico de pizza:

4. Gráfico de linhas:

5. Gráfico de setor: 

6. Boxplot:

7. Histograma:

O que é a média aritmética?

Média aritmética simples

A média aritmética funciona como um cálculo em que somamos todos os elementos de um conjunto de dados conhecido e dividimos essa soma pelo total de elementos que esse conjunto possui. 

Média aritmética ponderada

Na média ponderada, multiplicamos o conjunto de dados que temos pelo peso, que é um valor conhecido. Depois disso, dividimos esse valor pela soma dos pesos, para obter a média ponderada. 

Não se preocupe, teremos exercícios de cálculo de médias adiante. 

O que é distribuição normal?

A distribuição normal é quando um evento aleatório independe de regras ou padrões que fazem ele ocorrer, como o lançamento de uma moeda ao ar. Nesse caso, a distribuição normal é muito utilizada na estatística para representar cenários do mundo real. Assim, a probabilidade de eventos também está associada a distribuições.

Vejamos a seguir quais os tipos de distribuição existem na estatística.

Quais os tipos de distribuição estatística discreta?

• Distribuição de Poisson

A distribuição de Poisson possui algumas condições para ser realizada:

1. A tentativa consiste em calcular o número de vezes, k, que um evento ocorrerá em determinado intervalo, que pode ser tempo, por exemplo. Assim, a probabilidade do evento ocorrer é igual para cada intervalo;
2. O número de experimentos em um intervalo é independente dos demais, ou seja, seus resultados não dependerão de resultados anteriores e posteriores.

O cálculo de Poisson é feito pela fórmula: 

A letra lambda (λ) seria taxa de ocorrência. Vejamos um exemplo a seguir:

Suponha que 360 erros de impressão estejam distribuídos aleatoriamente, segundo uma Poisson, em um livro de 180 páginas. Calcule a probabilidade de encontrar uma página com nenhum erro.

Resposta: Sendo X: número de erros encontrados em 1 página, devemos calcular o valor do nosso parâmetro:

• Distribuição Binomial

Vamos imaginar que podemos ter um experimento que terá tentativas independentes, ou seja, seus resultados não dependerão de resultados anteriores e posteriores. Em cada experimento, podemos ter sucesso (S) ou fracasso (F).

Sendo assim, para termos sucesso, a probabilidade será igual a “p”. Já para fracasso, será igual a “q”, sendo q=1-p. O experimento acima, chamamos de ensaio de Bernoulli. 

A fórmula para calcularmos binomial seria: 

Sendo k = sucessos e n-k = falhas. Vejamos um exemplo a seguir: 

Uma prova consta de 10 testes com 5 alternativas cada um, sendo apenas uma delas correta. Um aluno que nada sabe a respeito da matéria avaliada “chuta” uma resposta para cada teste. Qual é a probabilidade dele acertar exatamente 4 testes?

Resposta:
Probabilidade de acertar um teste (sucesso) = 1/5
Probabilidade de errar um teste (falha) = 4/5

1º, 2º e 3º Quartil: o que são quartis e como calcular?

Quando calculamos a mediana, obtemos o valor médio de um rol específico. No caso, a mediana seria igual ao segundo quartil e, a metade desses 50%, que seria 25%, seria o primeiro quartil. Já o terceiro quartil seria a mediana + 25%, sendo 75% do rol.

Vejamos a imagem a seguir, que exemplifica isso: 

Para o cálculo vamos imaginar o seguinte rol: 73 74 77 52 85 59 73 84 92. 

Ordenando ele ficará da seguinte forma: 52 59 73 73 74 77 84 85 92. 

No caso, a mediana será igual a 74, pois, é o elemento que fica no meio dos elementos, já que temos um número ímpar de dados. Ele também é o quartil 2.

Quartil 1 = [52 59 73 73] 74 77 84 85 92 → 59 + 73 / 2 → 66.

Quartil 3 = 52 59 73 73 74 [77 84 85 92] → 84 + 85 / 2 → 84.5.

Sendo assim, quartil 1 é 74, quartil 2 é 66 e, quartil 3 é 84.5. 

Distância Interquartil

A distância interquartil é calculada através da diferença entre o quartil 3 e o quartil 1. Utilizando o exemplo anterior → 84.5 – 66 = 18.5 → distância interquartil.

Sistemas lineares: o que são e quais os tipos?

O que são sistemas lineares?

Um sistema linear significa um conjunto de equações, que podem ter duas ou mais equações, com duas ou mais incógnitas envolvidas nele. Um exemplo de sistema linear seria o seguinte:

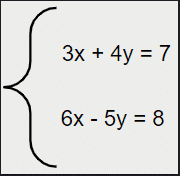
No exemplo acima, temos duas equações lineares com duas incógnitas, que no caso seriam x e y. Mas, o que seriam essas equações lineares? Elas serão abordadas no tópico seguinte.

O que é uma equação linear?

Uma equação linear seria quando precisamos encontrar valores que não conhecemos de incógnitas, sejam elas, x, y, z, a, etc. Uma equação precisa ter uma igualdade e ela é linear quando o maior expoente de suas incógnitas é igual a 1. Vejamos alguns exemplos: 

3x + 2y = 5 → equação linear com duas incógnitas (x e y).
-a + 8 = 3 → equação linear com uma incógnita (a).

Quais os tipos de sistemas lineares?

• Sistema possível determinado (SPD)

Um SPD seria quando o sistema possui apenas uma solução.

Vejamos o sistema linear a seguir: 

x + y = 5

4x – 2y = 2

Nele, vemos que só existe apenas uma solução que seria igual a (2,3) e, dessa forma, ele é classificado como SPD.

• Sistema possível indeterminado (SPI)

Um SPI seria quando o sistema possui infinitas soluções. 

Vejamos o sistema a seguir: 

x – y + z = 2

4x – 4y + 4z = 8

As soluções desse sistema podem ser infinitas, como (1, 0, 1), (0, 2, 4),…, e por isso classificamos ele como SPI.

• Sistema impossível (SI)

Um SI seria quando o sistema não possui nenhuma solução.

Vejamos o sistema a seguir, como exemplo: 

3x – 3y = – 9

3x – 3y = 15

Nesse caso, não existirá nenhuma solução para o sistema acima, pois nenhum par de números resolverá ele. Por isso, classificamos o sistema como SI.  

Não se preocupe, pois, será demonstrado como é feita a resolução de um sistema linear, nos exercícios adiante. 

 Média, moda e mediana: conheça as medidas de tendência central!

Média

A média, na estatística, é igual a média que você tira na escola, após o fim de um bimestre ou trimestre. Ela é calculada somando os valores de um conjunto de dados específico e, esses valores são divididos pelo número total de elementos que esse conjunto de dados possui.

Exemplo de média

Vamos ver um exemplo prático de média: suponhamos que você tenha tirado as seguintes notas em um bimestre: 5, 6, 7, 7. Sua média será a soma desses números (5, 6, 7 e 7), dividido por 4 (que seria o total de notas daquele bimestre). Como resultado, sua média será igual a 6.25.

Moda

A moda, significa, entre outras palavras, o elemento que mais aparece em um conjunto de dados. 

Exemplo de moda

Vamos analisar o caso anterior das médias: 5, 6, 7 e 7. A moda será igual ao 7, concorda? Pois, é a nota que aparece mais nesse conjunto de quatro valores acima. Ou seja, se em um conjunto de dados tenho um valor que aparece três vezes e outro que aparece duas, o valor que aparece três vezes é a moda daquele conjunto. 

Mediana

A mediana seria o elemento central que um conjunto de dados possui. Se a quantidade de números do conjunto de dados for par, a mediana é calculada através da média dos valores centrais. Se for ímpar, como 5, o valor será o valor do meio desse conjunto.

Exemplo de mediana

Para o caso das notas acima explicadas, os dados foram passados em ordem crescente, organizados. Mas, em alguns dados, as notas poderão vir como: 6, 7, 5, 7, ou seja, sem organização. O primeiro passo para calcular a mediana, seria ordenar os dados de forma crescente. 

Fazendo essa ordenação, os dados ficarão: 5, 6, 7, 7. Para calcular a mediana, calculamos a média dos valores centrais, que seriam 6 e 7, concorda? E a média é calculada pelos valores do conjunto dividido pela quantidade dos valores, correto? Sim! Ou seja, fazendo essa conta: (6+7/2), temos 6.5 como resultado da mediana. 

Amplitude, desvio, variância e desvio padrão: conheça as medidas de dispersão!

Para os exemplos das medidas de dispersão, utilizaremos o seguinte conjunto numérico: 

{2, 3, 4, 6, 1, 0, 9}.

Variância

A variância seria a soma de todos os quadrados do conjunto de dados que possuímos, dividindo ele pela quantidade de elementos do conjunto – 1. Ou seja, vamos pegar todos os elementos do conjunto acima, elevar eles ao quadrado e dividir eles por 6, já que temos 7 elementos e diminuímos 1, pela fórmula. 

Exemplo de variância

Vejamos a operação matemática que ficará com o exemplo acima: 

O resultado da variância, com base no exemplo acima, será igual a 24.5.

Desvio padrão

O desvio padrão dependerá da variância para ser calculado, pois ele é a raiz quadrada da variância. 

Exemplo de desvio padrão

Tirando a raiz quadrada da variância exibida anteriormente (24.5), temos como resultado: 4.95, aproximadamente, como desvio padrão. 

Amplitude

A amplitude é calculada através da diferença entre o maior e menor valor de um conjunto. 

Exemplo de amplitude

Observando o conjunto que utilizamos como exemplo, temos que o maior elemento é o 9 e o menor é o 0. Ou seja, se fizermos: 9 – 0, significa que a amplitude para esse caso, será igual a 9. 

Desvio 

O desvio, também chamado de desvio médio, é o cálculo do desvio em relação à média. Se os resultados dos desvios forem muito altos, a média é desprezada, pois não representa os dados do conjunto de forma coesa. Contudo, caso os desvios sejam baixos, a média é utilizada. 

O desvio é calculado através do módulo (que seria o caso que o número sempre dará positivo, independente se a subtração for 0 – 5, por exemplo) da subtração entre o valor do conjunto e a média dele. 

No conjunto que utilizamos, a média será igual a: 

Exemplo de desvio

Na tabela acima, é exibido o cálculo feito através do valor do conjunto menos a média, tendo como resultado o desvio, com base no conjunto utilizado. 

 5 exercícios de estatística resolvidos!

1. O número de pessoas atendidas no serviço de emergência de um hospital da cidade de Belo Horizonte, em todos os dias de novembro foi: 

15 23 12 10 28 7 12 17 20 21 18 13 11 12 26 30 6 16 19 22 14 17 21 28 9 16 13 11 16 20 

 Calcule a amplitude da distribuição.

Resposta: Organizando os dados de forma crescente, temos: 

6 7 9 10 11 11 12 12 12 13 13 14 15 16 16 16 17 17 18 19 20 20 21 21 22 23 26 28 28 30

A amplitude é calculada pela diferença entre o maior e o menor valor, ou seja,
30 – 6 = 24 → amplitude.

2. Calcule a média, a moda e a mediana dos números a seguir: 

133, 425, 244, 385, 236, 236, 328, 1000, 299, 325.

Organizando o rol: 133, 236, 236, 244, 299, 325, 328, 385, 425, 1000.

Resposta: Moda → como é a que mais aparece no conjunto, ela é o número 236. 

Média = 133 + 425 + 244 + 385 + 236 + 236 + 328 + 1000 + 299 + 325/10 = 361,1.

Mediana: 133, 236, 236, 244, 299, 325, 328, 385, 425, 1000

299 + 325/2 = 624/2 = 312.

3. Resolva o seguinte sistema linear a seguir e classifique-o em SPI, SPD, ou SI.

Resposta: 

i) Isolando uma incógnita:

x + y = 78
x = 78 – y.

ii) adicionando ela na outra equação:

x + 2y = 110
78 – y + 2y = 110
y = 32.

ii) substituindo o valor de y na outra equação:

x + y = 78
x + 32 = 78
x = 46. 

4. Calcule a média ponderada aproximada da nota bimestral do aluno, com base na tabela a seguir: 

Resposta: (MP = Média Ponderada)

MP = 6·4 + 7·4 + 8·2 + 9·2
                4 + 4 + 2 + 2

MP = 24 + 28 + 16 + 18
                      12

MP = 86
        12

MP = 7,2

5. Complete a tabela a seguir, com a frequência acumulada e relativa:

Livros	Frequência absoluta	Frequência acumulada	Frequência relativa
0	2
1	1
2	3
3	2
Total:	200	————–	————

Resposta: 

Livros	Frequência absoluta	Frequência acumulada	Frequência relativa
0	25	25	25/200 x 100 = 12,5%
1	30	55 (25+30)	30/200 x 100 = 15%
2	55	110 (55+55)	55/200 x 100 = 27,5%
3	90	200 (110+90)	90/200 x 100 = 45%
Total:	200	————–	—————-

 Como é o curso de estatística?

O curso de estatística tem uma duração de quatro anos e possibilita ao aluno ou aluna que possa interpretar e analisar dados do mundo real de forma simples. Como é uma matéria que envolve muitos cálculos, ela tem uma quantidade muito grande de conteúdos práticos. Alguns deles seriam os seguintes: 

• Probabilidade; 
• Álgebra Linear;
• Equações;
• Análise exploratória de dados;
• Modelagem de dados;
• Técnicas de Amostragem;
• Dentre outros. 

Quanto custa uma faculdade de estatística?

O valor médio de uma mensalidade de um curso de estatística gira em torno de 560 reais. Ou seja, em um ano, você pagaria mais de 6000 reais, para um ano de mensalidade girando em torno desse valor acima citado.

 Como está o mercado de trabalho para um profissional formado em estatística?

O mercado de trabalho está muito aquecido para quem segue nessa área, pois, essa profissão é uma das mais requisitadas do Brasil. Os segmentos que necessitam mais de atuação profissional seriam o da Meteorologia e o da Bioestatística, por exemplo. 

Ou seja, se você deseja trabalhar com estatística, além de ter a possibilidade de receber um salário alto, você também tem a possibilidade de trabalhar para empresas de grande porte e ser uma pessoa profissional requisitada no mercado. A estatística contribui não só para seu desenvolvimento profissional, como pessoal. 

Muito bacana o assunto sobre estatística, não acha? Esse assunto está muito presente em nosso cotidiano, pois, se formos parar para pensar, existe estatística para previsão do tempo, para um jogo de futebol, etc. Ela também está disponível em jogos de loteria, tais como a Mega Sena, para calcular a chance que uma pessoa tem de ganhar um prêmio gigante. 

Vimos alguns conceitos básicos de estatística, tais como tirar médias simples, ponderadas e, além disso, foi abordado o conteúdo de medidas de dispersão e medidas de tendência central, apresentando um exemplo prático para melhor entendimento delas. 

Para que o seu aprendizado em estatística seja contínuo, confira este artigo sobre o uso de fórmulas no Excel.