A classificação por bolha, ou Bubble Sort, é um algoritmo básico para organizar uma sequência de números ou outros elementos na ordem correta. O método funciona examinando cada conjunto de elementos adjacentes na string, da esquerda para a direita, trocando suas posições se estiverem fora de ordem. O algoritmo então repete esse processo até que possa percorrer toda a string e não encontrar dois elementos que precisem ser trocados.
Vamos conhecer mais sobre esse algoritmo? Então, confira o conteúdo que preparamos para você sobre o assunto:
- O que é o Bubble Sort e para que serve?
- Como e por que os programas de computadores usam Bubble Sort?
- Como o Bubble Sort funciona? Entenda com exemplos na prática!
- Quais as vantagens de usar o Bubble Sort?
- Quais as desvantagens de usar o Bubble Sort?
- Quais os outros algoritmos de ordenação mais usados?
O que é o Bubble Sort e para que serve?
Bubble Sort é um algoritmo de classificação comumente usado em ciência da computação. O Bubble Sort baseia-se na ideia de comparar repetidamente pares de elementos adjacentes e, em seguida, trocar as suas posições se existirem na ordem errada.
Algoritmo de classificação de bolhas:
- Em uma matriz não classificada de 5 elementos, comece com os dois primeiros elementos e classifique-os em ordem crescente. (Compare o elemento para verificar qual é o maior).
- Compare o segundo e o terceiro elemento para verificar qual é o maior e classifique-os em ordem crescente.
- Compare o terceiro e o quarto elemento para verificar qual é o maior e classifique-os em ordem crescente.
- Compare o quarto e o quinto elemento para verificar qual é o maior e classifique-os em ordem crescente.
- Repita as etapas 1–5 até que não sejam necessárias mais trocas.
Abaixo está uma imagem de uma matriz que precisa ser classificada. Usaremos o algoritmo de classificação de bolhas para classificar esta matriz:
Provavelmente, o algoritmo de classificação mais famoso é a classificação por bolha. Vale ressaltar que existem milhares de mutações a partir dele, e é usado principalmente para fins educacionais — como o primeiro algoritmo que você aprende.
Então, qual é o tipo de bolha? Imagine que estamos pegando os dois primeiros elementos. Se o primeiro elemento for maior que o segundo, nós os trocamos. Agora pegamos o segundo e o terceiro elementos — repetimos. Assim, no final, o maior elemento será o último membro da matriz. Agora, repetimos a operação para os primeiros n-1 números, portanto n-2 e assim por diante.
O código é incrivelmente simples:
var bubble_sort_classic = function (array) {
var length = array.length;
for (var i = 0; i <comprimento; i ++) {
for (var j = 0; j <comprimento - i - 1; j ++) {
if (matriz [j]> matriz [j + 1]) {
array.swap (j, j + 1);
}
}
}
array de retorno;
};
Vamos entender mais profundamente a seguir:
Qual é a aparência de um tipo de bolha?
Se uma pessoa programadora ou analista quisesse organizar uma série de números em ordem crescente, a abordagem de classificação por bolha seria semelhante ao exemplo ilustrado aqui.
O algoritmo revistaria dois itens por vez, reorganizaria aqueles que ainda não estavam em ordem crescente, da esquerda para a direita, e então continuaria a percorrer toda a sequência até completar uma passagem sem trocar nenhum número.
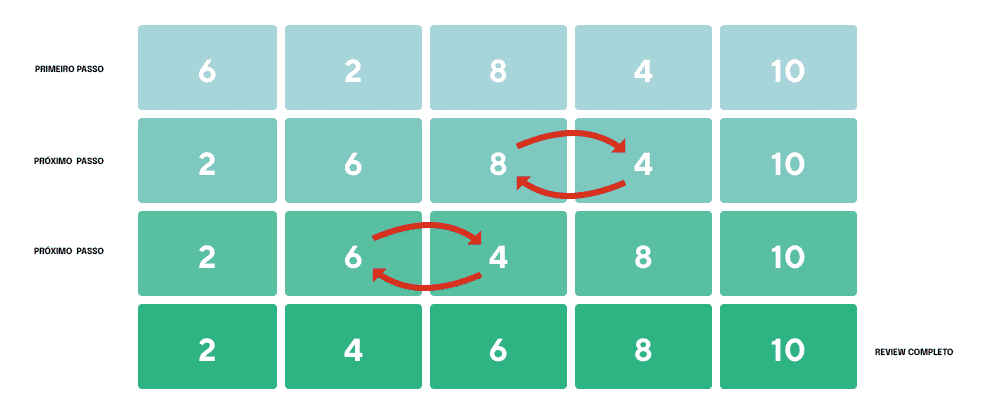
Como e por que os programas de computadores usam Bubble Sort?
Os programadores de computador usam a classificação por bolha para organizar uma sequência de números na ordem correta. Por ser o tipo mais simples de algoritmo de classificação, a classificação por bolhas não é muito usada na ciência da computação do mundo real. Seus usos mais comuns para pessoas programadoras incluem o seguinte:
1. Uma maneira de aprender a classificação básica
A classificação por bolha funciona como um método para ensinar novos programadores e programadoras a classificar conjuntos de dados porque o algoritmo é simples de entender e implementar.
2. Uma metodologia para classificar pequenos conjuntos de dados
Por ter que circular repetidamente por todo o conjunto de elementos, comparando apenas dois itens adjacentes por vez, a classificação por bolha não é ideal para conjuntos de dados mais massivos. Mas pode funcionar bem ao classificar apenas um pequeno número de elementos.
3. Uma metodologia de classificação para conjuntos de dados que, em sua maioria, já estão em ordem
Finalmente, alguns cientistas da computação e analistas de dados usam o algoritmo como uma verificação final para conjuntos de dados que eles acreditam já estarem em ordem quase classificada.
Como o Bubble Sort funciona? Entenda com exemplos na prática!
Pegamos um array não classificado como nosso exemplo. A classificação por bolha leva Ο (n 2 ) tempo, então estamos mantendo-a curta e precisa.
A classificação por bolha começa com os dois primeiros elementos, comparando-os para verificar qual é o maior.
Nesse caso, o valor 33 é maior que 14, portanto, já está nos locais classificados. Em seguida, comparamos 33 com 27.
Descobrimos que 27 é menor que 33 e esses dois valores devem ser trocados.
A nova matriz deve ser semelhante a esta:
Em seguida, comparamos 33 e 35. Descobrimos que ambos já estão em posições ordenadas.
Em seguida, passamos para os próximos dois valores, 35 e 10.
Sabemos então que 10 é menor que 35. Portanto, eles não são classificados.
Trocamos esses valores. Descobrimos que atingimos o final da matriz. Após uma iteração, o array deve ficar assim:
Para ser mais preciso, agora estamos mostrando como um array deve ficar após cada iteração. Após a segunda iteração, deve ficar assim:
Observe que após cada iteração, pelo menos um valor se move no final.
E quando não há necessidade de troca, o bubble sort aprende que um array está completamente classificado.
Exemplo de uso do Bubble Sort com Python
Agora que já entendemos a técnica, vamos à um exemplo de uso do Bubble Sort com Python.
def bubble_sort(list1):
# Outer loop for traverse the entire list
for i in range(0,len(list1)-1):
for j in range(len(list1)-1):
if(list1[j]>list1[j+1]):
temp = list1[j]
list1[j] = list1[j+1]
list1[j+1] = temp
return list1
list1 = [5, 3, 8, 6, 7, 2]
print("The unsorted list is: ", list1)
# Calling the bubble sort function
print("The sorted list is: ", bubble_sort(list1))
A lista não ordenada é: [5, 3, 8, 6, 7, 2]
A lista ordenada é: [2, 3, 5, 6, 7, 8]
Explicação:
No código acima, definimos uma função bubble_sort () que recebe list1 como um argumento.
Dentro da função, definimos dois loops for — primeiro o loop for itera a lista completa e o segundo loop for itera a lista e compara os dois elementos em cada iteração do loop externo.
O loop for será encerrado quando atingir o final.
Definimos a condição no loop for interno; se um primeiro valor de índice for maior que o segundo valor de índice, troque suas posições entre si.
Chamamos a função e passamos uma lista; iterou e retornou a lista classificada.
Sem usar uma variável temporária
Também podemos trocar os elementos sem usar a variável temp. Python tem uma sintaxe única. Podemos usar as seguintes linhas de código.
def bubble_sort (list1):
# Loop externo para percorrer toda a lista
para i no intervalo (0, len (lista1) -1):
para j no intervalo (len (lista1) -1):
if (lista1 [j] > lista1 [j + 1]):
# aqui não estamos usando a variável temporária
lista1 [j], lista1 [j + 1] = lista1 [j + 1], lista1 [j]
lista de retorno 1
lista1 = [5, 3, 8, 6, 7, 2]
print ("A lista não classificada é:", lista1)
# Chamando a função de classificação por bolha
print ("A lista classificada é:", bubble_sort (list1))
Saída:
A lista não ordenada é: [5, 3, 8, 6, 7, 2]
A lista ordenada é: [2, 3, 5, 6, 7, 8]
Exemplo de uso do Bubble Sort com C
/ * Programa C de Bubble Sort em ordem crescente. * /
#include <stdio.h>
int main()
{
int data[100],i,n,step,temp;
printf("Digite o número de elementos que deseja ordenar: ");
scanf("%d",&n);
for(i=0;i<n;++i)
{
printf("%d. Insira o elemento aqui:",i+1);
scanf("%d",&data[i]);
}
for(step=0;step<n-1;++step)
for(i=0;i<n-step-1;++i)
{
if(data[i]>data[i+1]) /* Se você deseja classificar em ordem decrescente, altere> para <apenas aqui. */
{
temp=data[i];
data[i]=data[i+1];
data[i+1]=temp;
}
}
printf("Em ordem crescente:");
for(i=0;i<n;++i)
printf("%d ",data[i]);
return 0;
}
Insira o número de elementos que deseja classificar: 9
Insira o elemento aqui: 12
Insira o elemento aqui: 3
Insira o elemento aqui: 0
Insira o elemento aqui: -11
Insira o elemento aqui: 1
Insira o elemento aqui: 4
Insira o elemento aqui: 9
Insira o elemento aqui: -2
Insira o elemento aqui: -6
Em ordem crescente: -11 -6 -2 0 1 3 4 9 12
Neste exemplo de classificação por bolha em C, primeiro, a pessoa usuária é solicitada a inserir o número total de elementos a serem inseridos na estrutura de dados. Usando um loop, os elementos de dados são inseridos. Os elementos são então comparados para classificação.
Se a condição if (data [i]> data [i + 1]), for verdadeira para qualquer iteração, os elementos são trocados e o loop passa para a próxima comparação. Quando todos os elementos da lista são comparados, a saída final classificada é impressa na tela após o término da comparação entre todos os elementos da estrutura de dados. Aqui, o número de elementos (n) é 9, então as etapas da classificação serão (n-1), ou seja, 8.
Exemplo de uso do Bubble Sort com Javascript
// Implementação de classificação de bolhas usando Javascript
// Criando a função bblSortfunction bblSort(arr){
for(var i = 0; i < arr.length; i++){
// Os elementos do último i já estão no lugar
for(var j = 0; j < ( arr.length - i -1 ); j++){
// Verificando se o item na iteração atual // é maior que a próxima iteração
if(arr[j] > arr[j+1]){
// Se a condição for verdadeira, troque-os
var temp = arr[j]
arr[j] = arr[j + 1]
arr[j+1] = temp
}
}
}
// Imprime a matriz (array) classificada
console.log(arr);
}
// Este é o nosso array não classificado
var arr = [234, 43, 55, 63, 5, 6, 235, 547];
// Agora passe este array para a função bblSort ()
bblSort(arr);
Saída
Matriz ordenada:
[5, 6, 43, 55, 63, 234, 235, 547]
Observação: a solução acima não se encontra otimizada ainda. A seguir, vamos conferir uma que está otimizada.
Solução Otimizada
Vejamos agora como é possível realizar um algoritmo de bubble sort em Javascript.
BubbleSort (array) {
para i -> 0 para arrayLength
isSwapped <- falso
para j -> 0 a (arrayLength - i - 1)
se arr [j]> arr [j + 1]
troca (arr [j], arr [j + 1])
isSwapped -> true
}
Implementação
function bubbleSort(arr){
var i, j;
var len = arr.length;
var isSwapped = false;
for(i =0; i < len; i++){
isSwapped = false;
for(j = 0; j < len; j++){
if(arr[j] > arr[j + 1]){
var temp = arr[j]
arr[j] = arr[j+1];
arr[j+1] = temp;
isSwapped = true;
}
}
// SE nenhum elemento foi trocado pelo loop interno, então quebre
if(!isSwapped){
break;
}
}
console.log(arr)
}
var arr = [243, 45, 23, 356, 3, 5346, 35, 5];
// chamando a função bubbleSortbubbleSort (arr)
Matriz classificada de saída :
[3, 5, 23, 35, 45, 243, 356, 5346]
Complexidades
Complexidade de tempo de pior caso e caso médio
Se a matriz estiver na ordem inversa, essa condição é o pior caso e sua complexidade de tempo é O (n 2 ).
Melhor caso de complexidade de tempo
Se a matriz já estiver classificada, então é o melhor cenário e sua complexidade de tempo é O (n)
Espaço Auxiliar : O (1)
Quais as vantagens de usar o Bubble Sort?
Uma das principais vantagens de um tipo de bolha é que ele é um algoritmo muito simples de ser descrito para um computador. Na verdade, há apenas uma tarefa a ser executada (compare dois valores e, se necessário, troque-os). Isso o torna um programa de computador muito pequeno e simples.
Quais as desvantagens de usar o Bubble Sort?
Bubble Sort é um dos algoritmos mais amplamente discutidos, simplesmente por causa de sua falta de eficiência para classificar matrizes. Se um array já estiver classificado, Bubble Sort passará pelo array apenas uma vez (usando o conceito dois abaixo), no entanto, o pior cenário é um tempo de execução de O (N²), que é extremamente ineficiente.
Quais os outros algoritmos de ordenação mais usados?
Alguns dos algoritmos de classificação mais comuns são:
- Selection sort
Na ordenação por seleção, o menor valor entre os elementos não classificados da matriz é selecionado em cada passagem e inserido em sua posição apropriada na matriz. É também o algoritmo mais simples. É um algoritmo de classificação de comparação no local. Neste algoritmo, a matriz é dividida em duas partes, a primeira é a parte classificada e a outra é a parte não classificada. Inicialmente, a parte classificada do array está vazia e a parte não classificada é o array fornecido. A parte classificada é colocada à esquerda, enquanto a parte não classificada é colocada à direita.
Na ordenação por seleção, o primeiro menor elemento é selecionado da matriz não ordenada e colocado na primeira posição. Depois que o segundo menor elemento é selecionado e colocado na segunda posição. O processo continua até que a matriz esteja totalmente classificada.
A complexidade média e de pior caso de ordenação por seleção é O (n 2 ) , onde n é o número de itens. Devido a isso, não é adequado para grandes conjuntos de dados.
- Insertion sort
A classificação por inserção funciona de maneira semelhante à classificação das cartas de baralho nas mãos. Presume-se que a primeira carta já está classificada no jogo de cartas e, em seguida, selecionamos uma carta não classificada. Se o cartão não classificado selecionado for maior que o primeiro cartão, ele será colocado no lado direito; caso contrário, ele será colocado no lado esquerdo. Da mesma forma, todas as cartas não classificadas são retiradas e colocadas em seus lugares exatos.
A mesma abordagem é aplicada na classificação por inserção. A ideia por trás da classificação por inserção é que primeiro pegue um elemento e itere-o por meio da matriz classificada. Embora seja simples de usar, não é apropriado para grandes conjuntos de dados, pois a complexidade do tempo de classificação de inserção no caso médio e o pior caso é O (n 2 ) , onde n é o número de itens. A classificação por inserção é menos eficiente do que outros algoritmos de classificação, como classificação heap, classificação rápida, classificação por mesclagem, etc
- Merge sort
A classificação por mesclagem é semelhante ao algoritmo de classificação rápida, pois usa a abordagem dividir e conquistar para classificar os elementos. É um dos algoritmos de classificação mais populares e eficientes. Ele divide a lista fornecida em duas metades iguais, chama a si mesmo para as duas metades e, em seguida, mescla as duas metades classificadas. Temos que definir a função merge () para realizar a fusão.
As sublistas são divididas repetidas vezes em metades até que a lista não possa ser mais dividida. Em seguida, combinamos o par de listas de um elemento em listas de dois elementos, classificando-as no processo. Os pares classificados de dois elementos são mesclados nas listas de quatro elementos e assim por diante até obtermos a lista classificada.
- Quick sort
A classificação é uma forma de organizar os itens de maneira sistemática. Quicksort é o algoritmo de classificação amplamente usado que faz n log n comparações em caso médio para classificar uma matriz de n elementos. É um algoritmo de classificação mais rápido e eficiente. Este algoritmo segue a abordagem de dividir para conquistar. Dividir para conquistar é uma técnica de quebrar os algoritmos em subproblemas, resolver os subproblemas e combinar os resultados novamente para resolver o problema original.
- Heap sort
A classificação de heap processa os elementos criando o heap mínimo ou heap máximo usando os elementos da matriz fornecida. Pilha mínima ou pilha máxima representa a ordem da matriz em que o elemento raiz representa o elemento mínimo ou máximo da matriz. Em cada etapa, o elemento raiz do heap é excluído e armazenado na matriz classificada e o heap será novamente heapificado.
- Bucket sort
A classificação de intervalo é um algoritmo de classificação que separa os elementos em vários grupos chamados de intervalos. Os elementos na classificação de intervalos são primeiro uniformemente divididos em grupos chamados de intervalos e, em seguida, são classificados por qualquer outro algoritmo de classificação. Depois disso, os elementos são reunidos de forma ordenada.
O ponto forte do Bubble Sort é a sua simplicidade. Leva apenas algumas linhas de código, é fácil de ler e pode ser conectado em qualquer lugar do programa. No entanto, é extremamente ineficiente para conjuntos maiores de números e deve ser usado de acordo.
Aprenda agora sobre Clojure, o que é e para que serve essa linguagem de programação!


