Algoritmo de dijkstra: como calcular o caminho de custo mínimo?

Nos dias de hoje somos capazes de traçar as rotas mais eficazes em uma cidade a partir do GPS, que por debaixo dos panos utiliza o algoritmo de dijkstra.

Ao tentarmos implementar este algoritmo em alguma linguagem de programação, podemos ter problemas em entender o seu funcionamento.

Portanto, em nossos tópicos, mostraremos o quão simples e didático o algoritmo de dijkstra consegue ser, desta maneira, você pode até tentar recriar o algoritmo na sua linguagem de programação preferida. Confira:

• O que é o Algoritmo de dijkstra?
• Como surgiu e quem criou o Algoritmo de dijkstra?
• O que são Grafos?
• O que são Grafos ponderados?
• Quais os tipos de Grafos?
• Como funciona o Algoritmo de dijkstra? Passo a passo e diagrama!
• Exemplo de uso do Algoritmo de dijkstra em JavaScript

O que é o Algoritmo de dijkstra?

O algoritmo de dijkstra tem o objetivo de encontrar o menor caminho entre dois grafos que estão conectados. Hoje em dia é muito utilizado em sistemas que utilizam o GPS, como o Google Maps, Uber, 99, etc.

Resumidamente, temos que o algoritmo percorre todos os caminhos possíveis entre as duas localizações e retorna qual o menor caminho possível.

Como surgiu e quem criou o Algoritmo de dijkstra?

Foi criado em 1956 pelo Edsger Dijkstra, um cientista da computação holandês. Em 1959 foi publicado oficialmente e, desde então, ficou muito conhecido e passou a ser amplamente utilizado.

Seu criador, um grande matemático, contou em uma entrevista que pensou no algoritmo enquanto estava fazendo compras com a esposa, e percebeu que poderia encontrar o menor caminho entre duas localidades. Ele também conta que precisou de apenas 20 minutos para criá-lo.

O que são Grafos?

Grafos são um tipo de estruturas de dados que representam a conexão de par entre elementos. Chamamos esses elementos de nós. Eles podem ser pessoas, cidades, objetos, qualquer coisa. A conexão de nós é chamada de arestas.

Um grafo pode ser representado da seguinte forma:

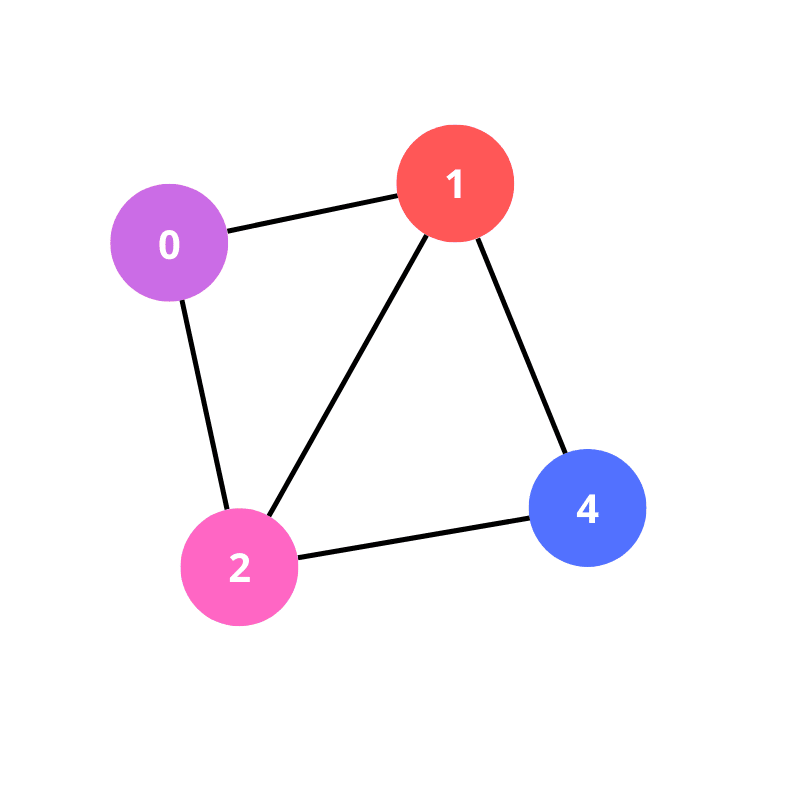
Nós

Os nós são as figuras redondas coloridas com números.

Arestas

Já as arestas são as linhas que realizam a conexão entre si.

O que são Grafos ponderados? 

Um grafo ponderado tem em cada aresta um valor que pode equivaler a distância de duas localizações ou outra representação numérica, por exemplo.

Na imagem abaixo, podemos ver os números ao lado das arestas, em que cada dígito é a representação do valor das arestas. Dessa maneira, podemos concluir que este grafo é ponderado.

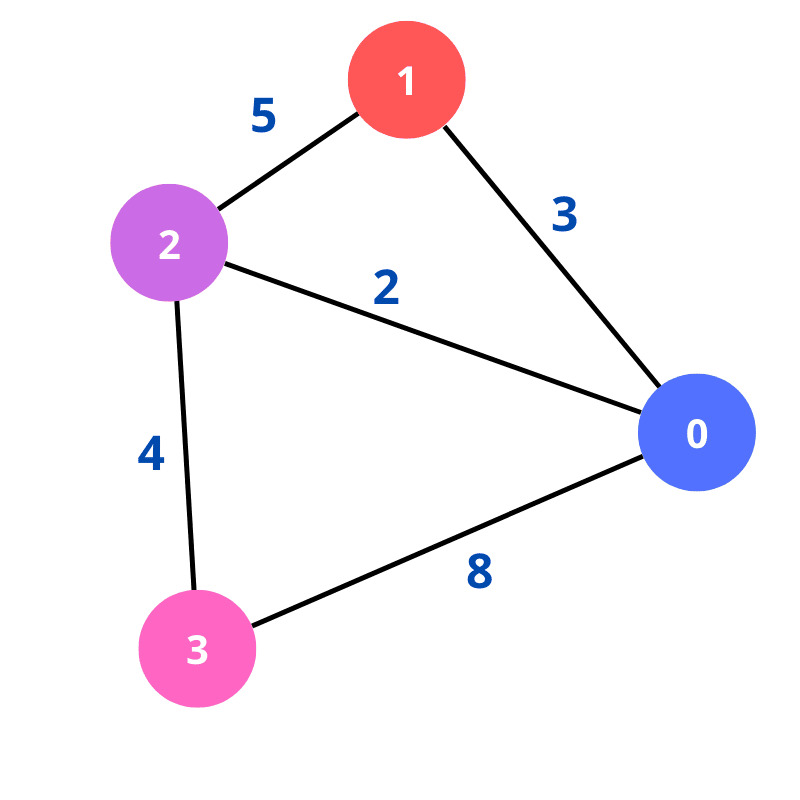
Os valores nas arestas são importantes para o algoritmo de dijkstra.

Quais os tipos de Grafos?

Além do grafo ponderado, temos outros dois tipos de grafos que são bem populares e usados no mundo real.

Dirigidos 

Em um grafo dirigido, nós só podemos nos movimentar em uma direção estabelecida pela seta da aresta. Como vemos na imagem abaixo, o nó 0 só pode ir até o nó 1 ou nó 3, e o único jeito de voltar é indo até o nó 2 e depois pro nó 0 novamente.

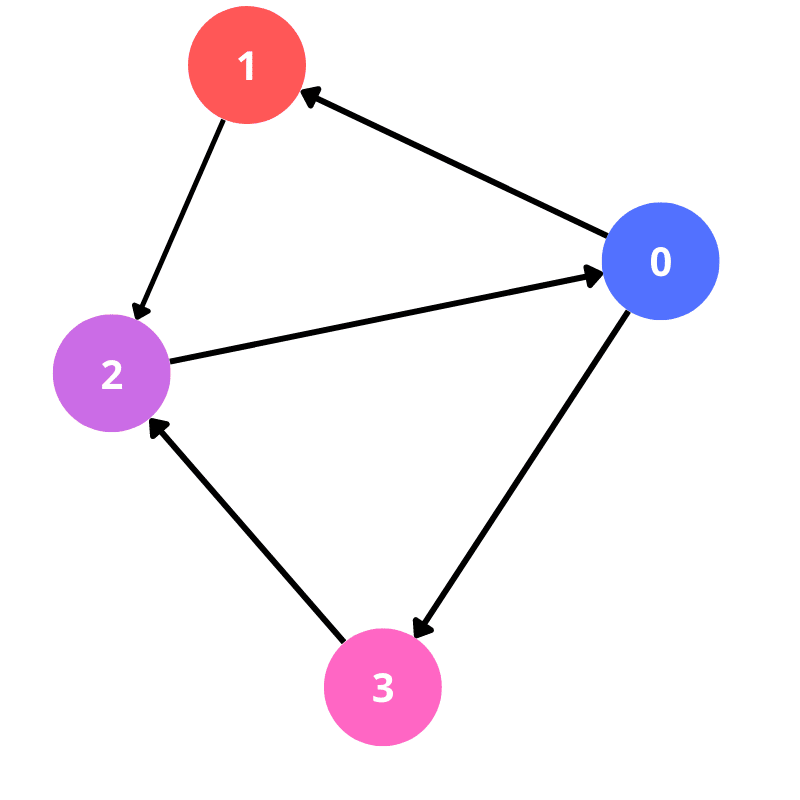
Não dirigidos

No grafo não dirigido podemos nos movimentar de um nó para outro em qualquer direção. A imagem abaixo representa isso:

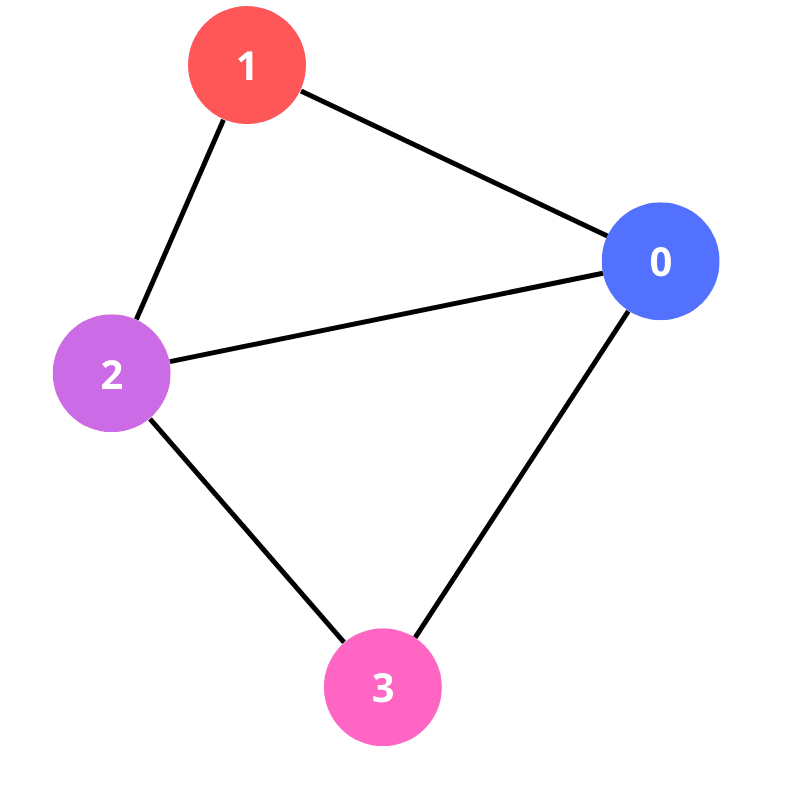
Como funciona o Algoritmo de dijkstra? Passo a passo e diagrama!

Agora que já entendemos um pouco mais sobre os grafos, conseguimos aplicar o algoritmo de dijkstra para a resolução de um problema.

Utilizaremos o grafo a seguir:

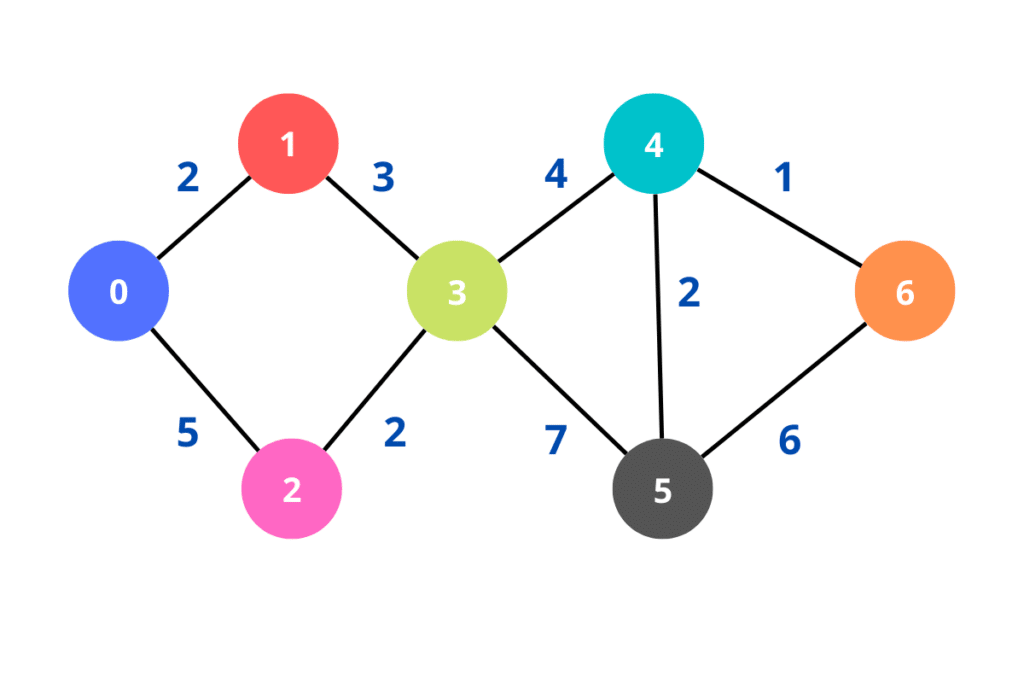
Neste exemplo, vamos descobrir as menores distâncias possíveis entre o nó 0 e todos os nós da figura. Deste modo, consideramos os valores das arestas como a distância destes nós. 

Para começarmos, definimos alguns pontos. A distância do nó inicial até ele mesmo é de 0 e, como ainda não calculamos a distância do nó inicial até os outros nós, deixamos o valor com o símbolo de infinito.

Distância do Nó inicial até o nó de número indicado:

0	0
1	∞
2	∞
3	∞
4	∞
5	∞
6	∞

Também temos uma lista que mostra os nós que ainda vão ser visitados:

• 0
• 1
• 2
• 3
• 4
• 5
• 6

Como já visitamos o nó 0, podemos adicionar um asterisco (*) ao lado do número. Além disso, no diagrama, vamos adicionar um círculo no nó 0, para ficar mais evidente a sua visita.

• 0 *
• 1
• 2
• 3
• 4
• 5
• 6

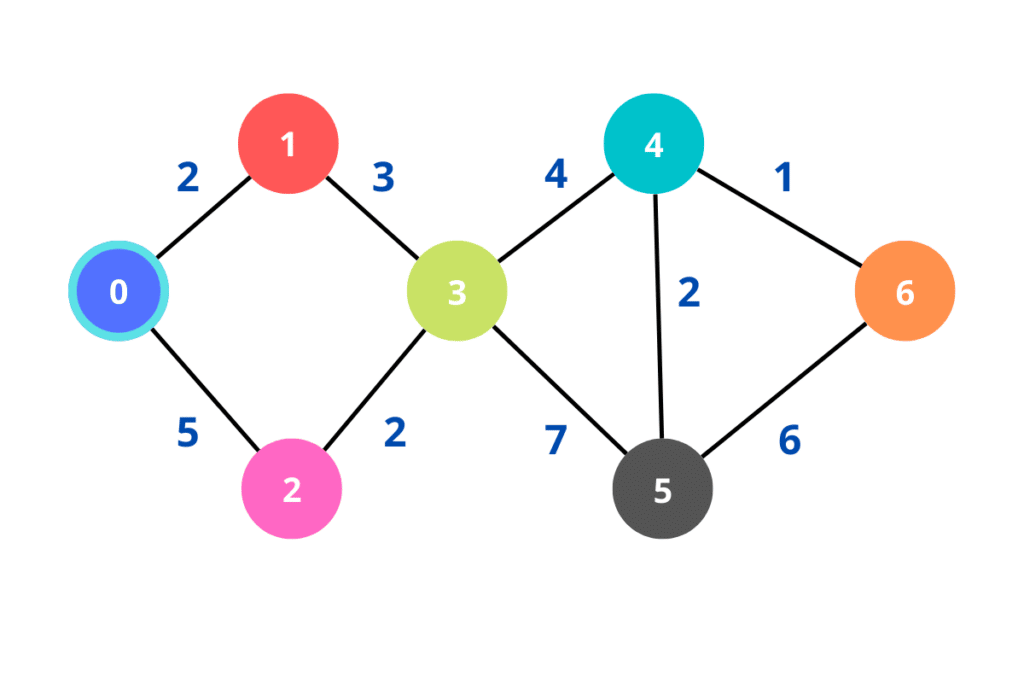
O próximo passo é verificar a distância do primeiro nó para os nós adjacentes, no caso o nó 1 e o nó 2.

As distâncias dos dois itens para o nó 0 são: 2 e 5, sendo assim, adicionamos esses valores na nossa tabela. 

0	0
1	2
2	5
3	∞
4	∞
5	∞
6	∞

A partir disso, vamos encontrar o menor valor entre os dois caminhos que conhecemos atualmente.

Em nosso caso, o nó 1 possui a menor distância (2) e por isso adicionamos como o melhor caminho atualmente.

Na figura adicionamos o círculo da cor azul claro em volta do nó.

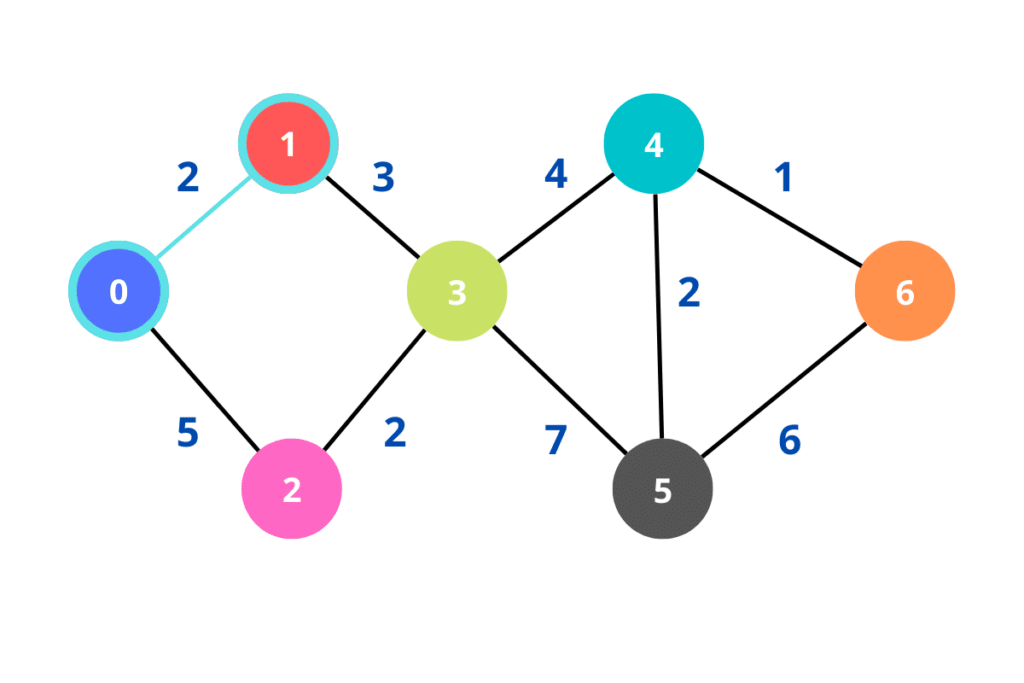
Na nossa tabela evidenciamos que o nó 1  foi visitado e possui o menor valor.

0	0
1	2 (nó 0 -> nó 1)
2	5
3	∞
4	∞
5	∞
6	∞

Também adicionamos o asterisco demonstrando que este nó foi visitado.

• 0 *
• 1 *
• 2
• 3
• 4
• 5
• 6

O próximo passo é verificar quais nós estão conectados ao próximo objeto, que é o nó 3.

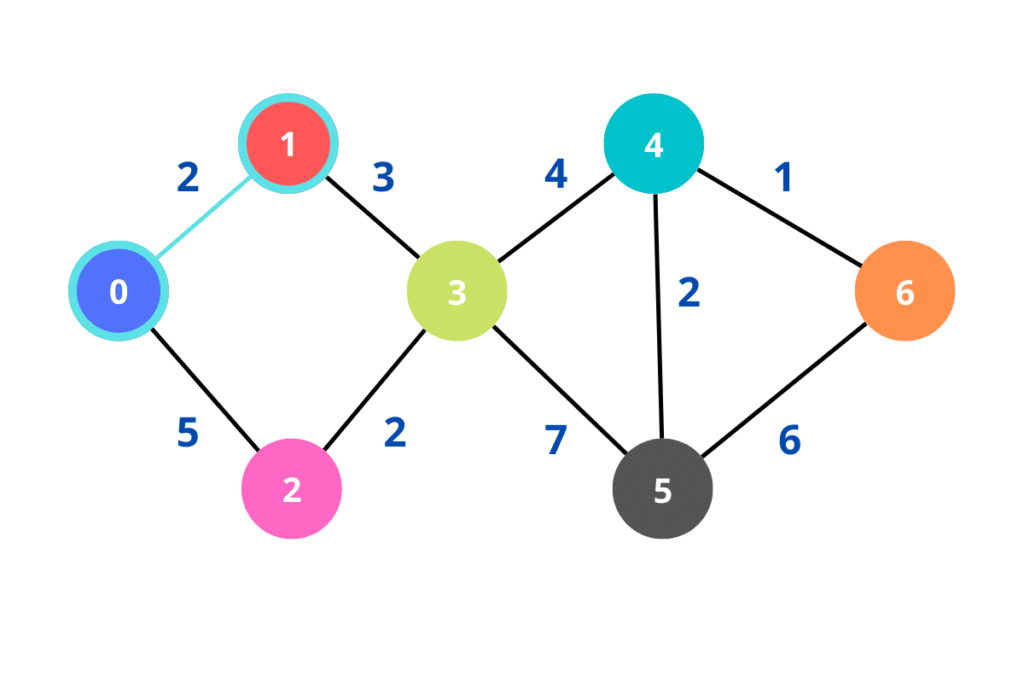
Como vemos na figura, o nó 2 também está conectado ao nó 3, sendo assim, ele é um possível candidato ao menor caminho possível.

Por causa disso, adicionamos em nossa tabela o caminho do nó 2 e também o marcamos na figura.

0	0
1	2 (nó 0 -> nó 1)
2	5 (nó 0 -> nó 2)
3	∞
4	∞
5	∞
6	∞

• 0 *
• 1 *
• 2 *
• 3
• 4
• 5
• 6

Para chegarmos ao nó 3 temos duas possibilidades: o caminho do nó 0 -> nó 1 -> nó 3 e o caminho do nó 0 -> nó 2 -> nó 3. Desse jeito, se repararmos na figura, o primeiro caminho possui o valor de 5 e o segundo o valor de 7. Logo, temos que o primeiro caminho é o menor.

Mesmo descobrindo que o nó 2 não será mais utilizado para realizar as conexões dos outros nós, deixaremos  ele marcado para demonstrar o menor caminho possível entre o nó 0 e o nó 2.

Continuamos marcando em nossa tabela e desenhamos no diagrama.

0	0
1	2 (nó 0 -> nó 1)
2	5 (nó 0 -> nó 2)
3	7 (nó 0 -> nó 1 -> nó 3)
4	∞
5	∞
6	∞

• 0 *
• 1 *
• 2 *
• 3 *
• 4
• 5
• 6

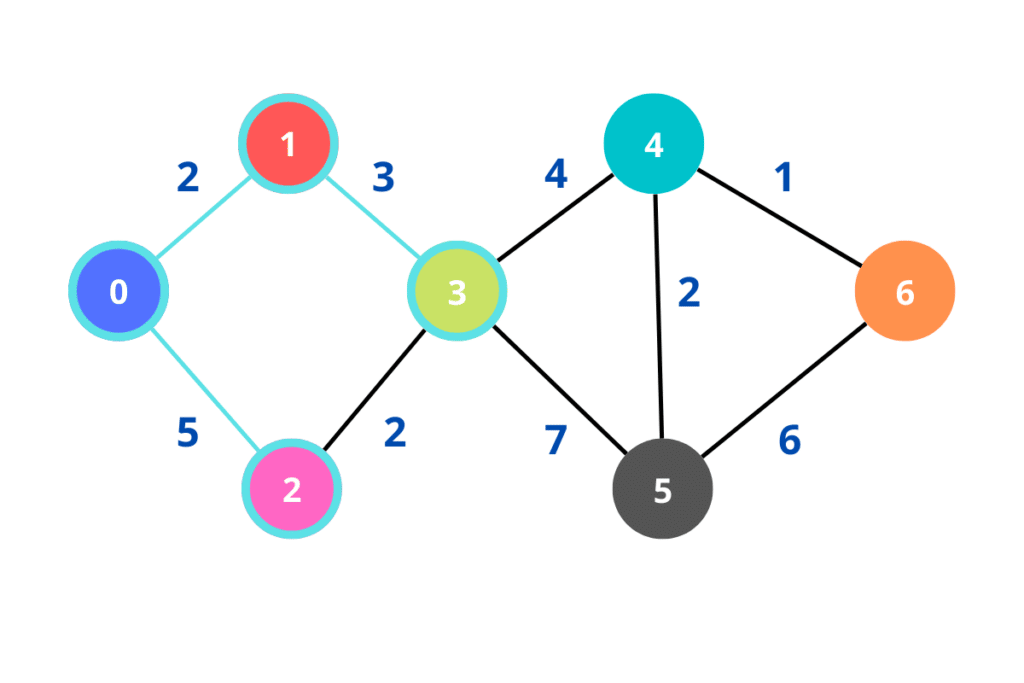
Agora que já estamos na metade do caminho fica muito mais fácil terminar. A partir do nó 3, os seus adjacentes são o nó 4 e o nó 5. Para o nó 4 existem duas possibilidades: o caminho do nó 0 -> nó 1 -> nó 3 -> nó 4 que possui a distância de 9 e o caminho do nó 0 -> nó 1 -> nó 3 -> nó 5 -> nó 4 que tem a distância de 14. Evidentemente, o primeiro caminho é o menor.

0	0
1	2 (nó 0 -> nó 1)
2	5 (nó 0 -> nó 2)
3	7 (nó 0 -> nó 1 -> nó 3)
4	9 (nó 0 -> nó 1 -> nó 3 -> nó 4)
5	∞
6	∞

• 0 *
• 1 *
• 2 *
• 3 *
• 4 *
• 5
• 6

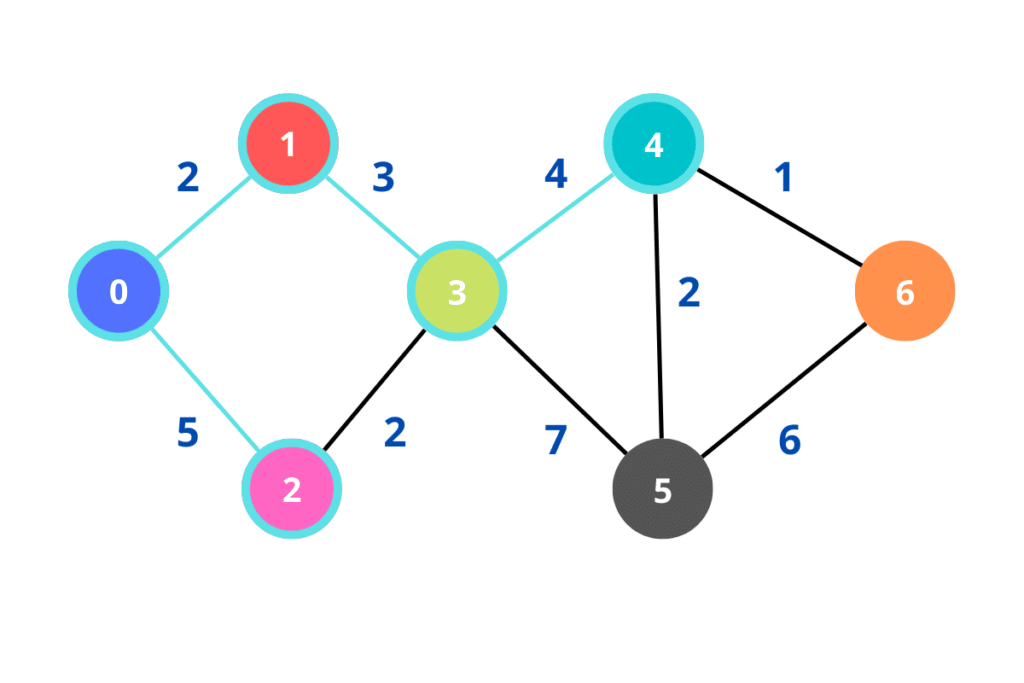
Para encontrarmos o menor caminho para o nó 5, temos o caminho do nó 0 -> nó 1 -> nó 3 -> nó 5, com o valor total de 12 e também o caminho do nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 5, com o valor total de 11. Concluímos que o segundo caminho é o menor.

Lembrando que não é possível utilizar o nó 2 em nosso caminho, já que constatamos que ele é mais distante que o nó 1, sendo assim não precisamos perder tempo calculando a sua distância para os outros nós.

0	0
1	2 (nó 0 -> nó 1)
2	5 (nó 0 -> nó 2)
3	7 (nó 0 -> nó 1 -> nó 3)
4	9 (nó 0 -> nó 1 -> nó 3 -> nó 4)
5	11 (nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 5)
6	∞

• 0 *
• 1 *
• 2 *
• 3 *
• 4 *
• 5 *
• 6

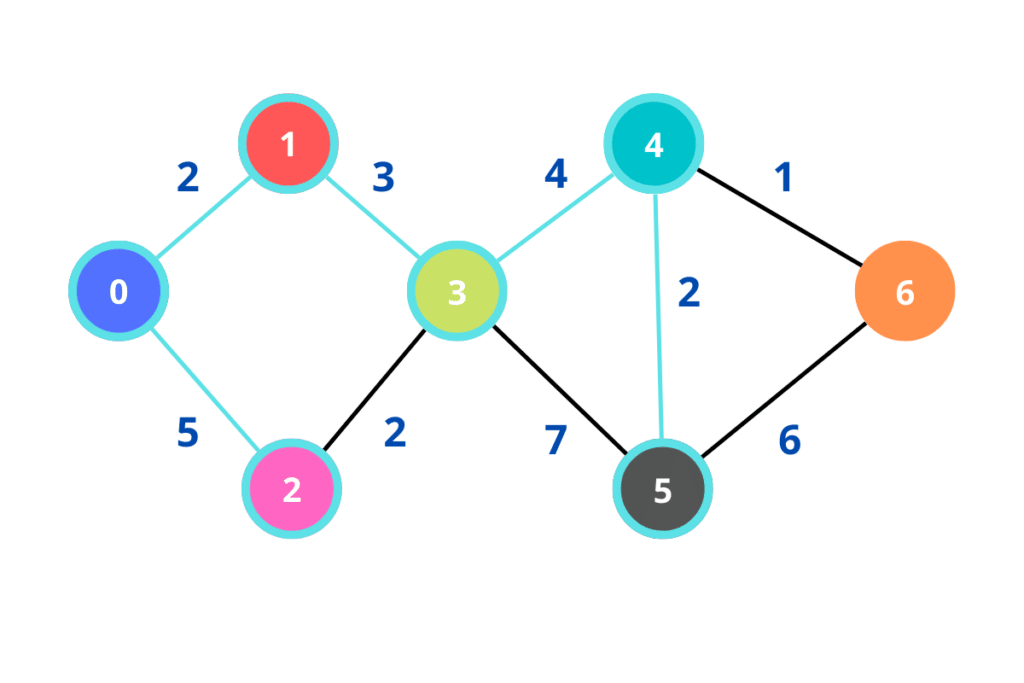
Para o último nó, contamos a distância do nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 6 com o valor 10 e também a distância do nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 5 -> nó 6 com valor 17. A primeira opção é a mais viável e, com isso, descobrimos os menores valores do nó 0 para todos os outros nós.

0	0
1	2 (nó 0 -> nó 1)
2	5 (nó 0 -> nó 2)
3	7 (nó 0 -> nó 1 -> nó 3)
4	9 (nó 0 -> nó 1 -> nó 3 -> nó 4)
5	11 (nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 5)
6	10 (nó 0 -> nó 1 -> nó 3 -> nó 4 -> nó 6)

• 0 *
• 1 *
• 2 *
• 3 *
• 4 *
• 5 *
• 6 *

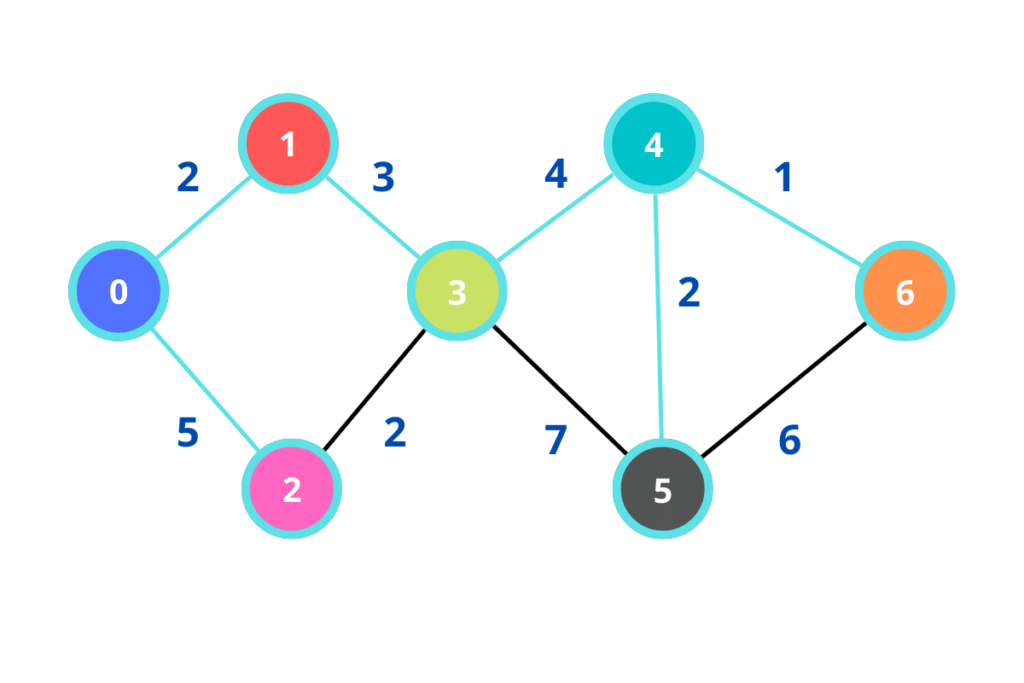
Exemplo de uso do Algoritmo de dijkstra em Javascript

Como já sabemos, o algoritmo de dijkstra pode ser descrito e visualizado em qualquer linguagem de programação. No nosso caso, vamos escrevê-lo em Javascript e mostrar como é simples recriar esta lógica.

Solucionaremos o seguinte grafo:

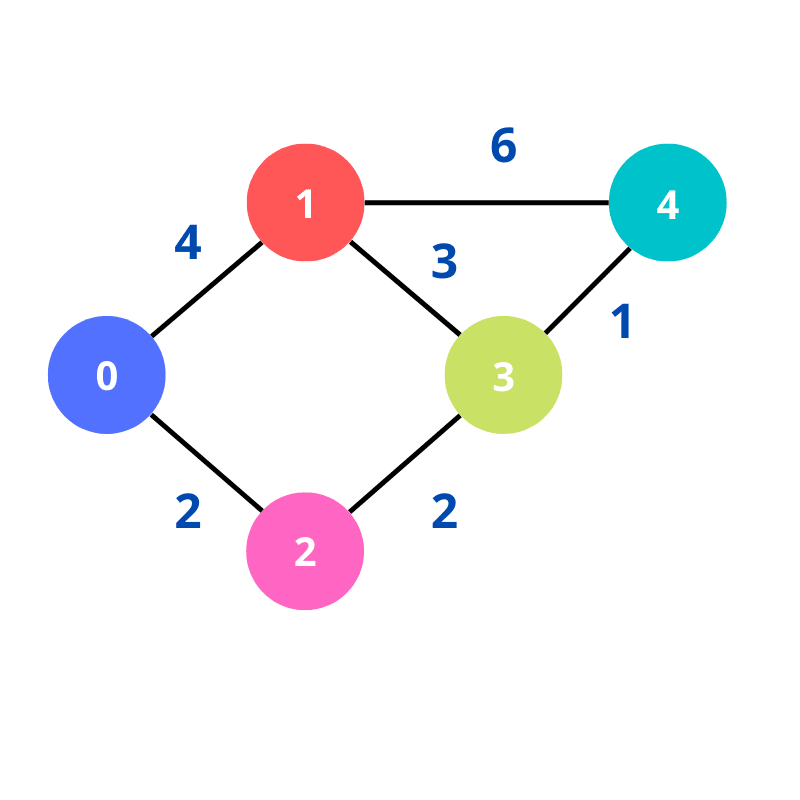
Antes de começarmos, verifique se você possui o Node instalado na sua máquina. Logo depois disso, basta que vocẽ crie um arquivo com o seguinte código:

class Grafo {
  constructor() {
    this.vertices = []
    this.graficoNos = {}
  }

  // Função para criar os nós do grafo
  addNo(no) {
    this.vertices.push(no);
    this.graficoNos[no] = []
  }

  // Função para adicionar arestas do grafo
  addAresta(no1, no2, distancia) {
    this.graficoNos[no1][no2] = distancia;
  }

  // Calcula a menor distância entre os nós visitados
  calcularNoMenorDistancia(distancias, visitados) {
    let minimaDistancia = Infinity,
      menorNo = null;
    for (let no in distancias) {
      let distancia = distancias[no];
      if (distancia < minimaDistancia && !visitados.has(no)) {
        minimaDistancia = distancia;
        menorNo = no;
      }
    }
    return menorNo;
  }

  // Função principal do algoritmo para encontrar a menor distância entre dois nós
  dijkstra(comeco, fim) {
    let distancias = {},
      visitados = new Set();
    
    // Adicionamos as distâncias iniciais dos nós
    for (let i = 0; i < this.vertices.length; i++) {
      if (this.vertices[i] === comeco) {
        distancias[comeco] = 0;
      } else {
        distancias[this.vertices[i]] = Infinity;
      }
    }

    let noAtual = this.calcularNoMenorDistancia(distancias, visitados);

    // Enquanto existir um nó para ser calculado a função irá se repetir
    // Nela comparamos os valores dos nós vizinhos e determinamos a menor distância entre eles
    while (noAtual !== null) {
      let distancia = distancias[noAtual],
        vizinhos = this.graficoNos[noAtual];
      for (let vizinho in vizinhos) {
        let novaDistancia = distancia + vizinhos[vizinho];
        if (distancias[vizinho] > novaDistancia) {
          distancias[vizinho] = novaDistancia;
        }
      }
      visitados.add(noAtual);
      noAtual = this.calcularNoMenorDistancia(distancias, visitados);
    }

    // Exibimos qual a distância mínima entre os dois nós
    console.log(`A distância mínima entre o nó ${comeco} e o nó ${fim} é ${distancias[fim]}`);
  }
}

// Criamos o nosso grafo
const grafo = new Grafo();

// Adicionamos as suas informações
grafo.addNo("0")
grafo.addNo("1")
grafo.addNo("2")
grafo.addNo("3")
grafo.addNo("4")
grafo.addAresta("0", "1", 4);
grafo.addAresta("0", "2", 2);
grafo.addAresta("1", "3", 3);
grafo.addAresta("1", "4", 6);
grafo.addAresta("2", "3", 2);
grafo.addAresta("3", "4", 1);

// Executamos a função principal
grafo.dijkstra("0", "4")

Abra o terminal no diretório atual e rode o comando node nome_do_arquivo.js, como por exemplo:

A resposta aparecerá logo abaixo da execução do comando.

Podemos representar o resultado do grafo da seguinte forma:

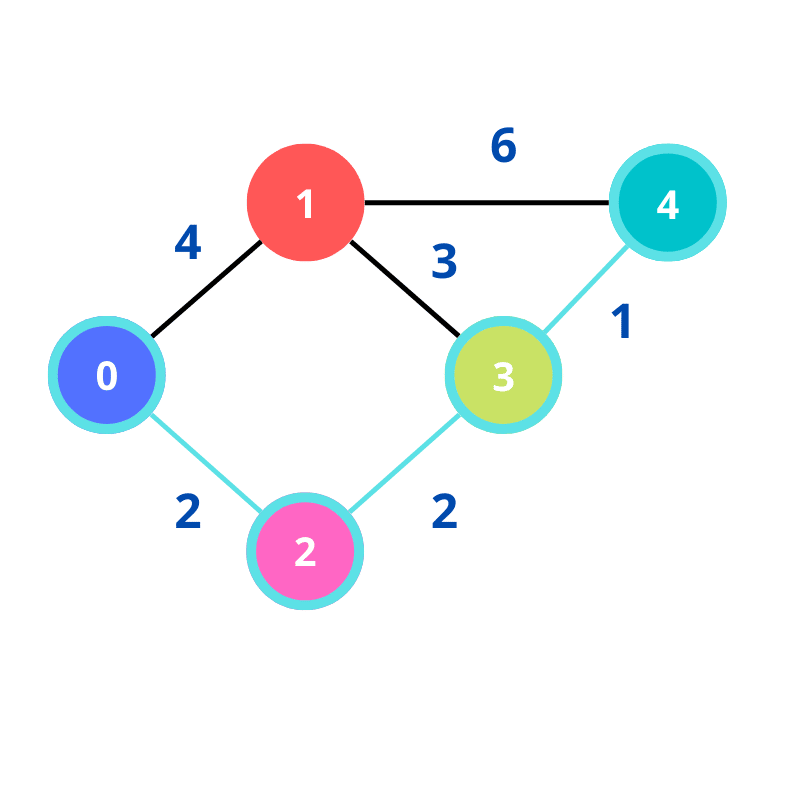
O algoritmo de dijkstra é muito popular na ciência da computação e resolve o problema de encontrar a menor distância entre dois pontos, seja pequenos objetos até grandes cidades. Esta lógica é empregada até os dias atuais em ferramentas como o GPS e aplicativos adjacentes, como é o caso do Google Maps.

Existem várias formas de construir um grafo. A partir disso, a lógica deste algoritmo se propõe a resolver os grafos dirigidos e não dirigidos que não têm valor negativo. 

Vale ressaltar que, por se tratar de um algoritmo, a sua lógica pode ser explicada em qualquer tipo de meio, seja no lápis e papel, em figuras digitais ou até mesmo nas linguagens de programação, como Java, C#, Javascript, C, etc. 

Se interessou pela ideia dos algoritmos? Então veja sobre Pseudocódigo: o que é e como é usado na programação?