Você já imaginou se todos os computadores que temos funcionassem utilizando numeração binária? Essa, no caso, seria a numeração entre 0 e 1, apenas. Não seria nada legal, concorda? Para isso, existe o sistema hexadecimal, que tem mais valores para serem representados e é muito utilizado para a construção de microprocessadores.
Contudo, algumas pessoas podem ter dificuldade para o entendimento do sistema hexadecimal como um todo, devido ao fato de que ele abrange várias conversões e vários valores para as dezesseis casas que ele possui em sua representação.
Porém, a manipulação desse sistema é muito mais simples conforme os números vão ficando maiores, e isso acaba facilitando não só na visualização dos números, mas também nas operações que serão feitas com ele. Ficou curioso para aprender mais sobre o sistema hexadecimal? Venha com a gente, pois explicaremos tudo sobre seu funcionamento! Confira:
- O que é o sistema Hexadecimal?
- Valores das casas do sistema Hexadecimal
- Quais os principais usos do sistema Hexadecimal?
- O que são os números com o prefixo “0x”? Hexadecimal na programação C
- Exemplos de uso de valores Hexadecimais na programação C
- Convertendo Hexadecimal para Decimal, Binário e Octal
- Quais as vantagens e desvantagens do sistema Hexadecimal?
O que é o sistema Hexadecimal?
O sistema hexadecimal é um sistema de numeração que possui base 16, ou seja, nesse sistema, são utilizados dezesseis símbolos. Esse sistema teve como base o sistema binário de numeração, pois, como já foi dito, seria muito difícil se somente dígitos binários (0 ou 1) fossem utilizados para construção de equipamentos eletrônicos.
Desse modo, os hexadecimais surgiram para facilitar a interação entre o ser humano e o computador, de forma que erros humanos fossem evitados no processo de desenvolvimento de equipamentos diversos.
Quais são os dezesseis símbolos utilizados nesse sistema? Eles são os seguintes:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Como você pode notar, são dez valores numéricos e seis letras, que representam os valores, totalizando dezesseis símbolos.
Ainda não entendeu completamente? Sem problemas. No próximo tópico, serão explicados os valores de cada casa que esse sistema de numeração possui.
Valores das casas do sistema Hexadecimal
Cada dígito hexadecimal corresponde a um grupo diferente de quatro dígitos binários. Ou seja, isso diminui a quantidade de numerais para representar um determinado número.
Vamos olhar a tabela a seguir para entender melhor o que foi explicado acima:
Vamos analisar alguns exemplos, com base na tabela acima:
- Se temos um binário de quatro dígitos e ele é representado por 0000, seu correspondente será 0;
- Se temos um binário de quatro dígitos e ele é representado por 0101, seu correspondente será 5;
- Se temos um binário de quatro dígitos e ele é representado por 1000, seu correspondente será 8;
- Se temos um binário de quatro dígitos e ele é representado por 1010, seu correspondente será a letra A;
- Se temos um binário de quatro dígitos e ele é representado por 1101, seu correspondente será a letra D;
- Se temos um binário de quatro dígitos e ele é representado por 1111, seu correspondente será a letra F;
Para entender o porquê do valor correspondente de 1000 ser igual a 8 no sistema hexadecimal, como ele é feito em base 2, elas seguem os seguintes valores:
E, para representar o algarismo 8, em binário, somente a casa que corresponde ao seu valor precisará estar preenchida:
Fique tranquilo que, nos próximos tópicos, essas conversões de sistemas diferentes serão explicadas. Mas, é importante que você tenha compreendido essa tabela, pois ela será o seu material de apoio para as operações que serão feitas.
Quais os principais usos do sistema Hexadecimal?
Abaixo, alguns principais usos dos hexadecimais:
- Você deve estar se perguntando: aqueles códigos que eu utilizo, nas folhas de estilos (CSS), para as cores em páginas web, são hexadecimais? Sim! Por exemplo, o código #FFF representa a cor branca nos sites, para você colorir um botão, um link em específico, etc. Ou seja, uma das aplicações do sistema hexadecimal seria a estilização de páginas web.
- Exibição de mensagens de erro, pois, ao definir para cada hexadecimal um código de erro, é mais fácil localizar o erro na memória e pesquisar sobre ele para ser corrigido;
Essas são as duas principais utilizações dos hexadecimais. Agora, verificaremos como ele funciona na linguagem de programação C.
O que são os números com o prefixo “0x”? Hexadecimal na programação C!
Números com o prefixo 0x indicam que o número que está representado é um hexadecimal. Por exemplo, uma pessoa verifica no manual de seu computador recém-comprado um símbolo “0xCD”, que equivale a um decimal de 205.
Ou seja, pelo símbolo “0x” estar na frente do “CD”, essa pessoa saberá que está trabalhando com hexadecimais. Mas, ela utilizará somente as letras “CD”, ao lado do prefixo “0x”, que é somente um indicativo que o número é um hexadecimal. Dessa forma, o 0x, para essa análise, é ignorado.
Exemplos de uso de valores Hexadecimais na programação C
No código abaixo exibido na linguagem C, por exemplo, se colocarmos a função %x, ao lado da impressão dos valores:
int main ( )
{
int decimal = 0x32 ;
int hexadecimal = 0xFDEC ;
printf ( " valor decimal: % X [ % x ] \ n " , decimal , decimal ) ;
printf ( " valor hexadecimal: % X [ % x ] \ n " , hexadecimal , hexadecimal ) ;
return 0 ;
}O resultado será o seguinte no compilador. Assim, ele desconsidera o 0x presente na variável, mesmo ela sendo declarada com o valor:
Outro exemplo que podemos utilizar seria um conversor de hexadecimal em decimal na linguagem C, utilizando o seguinte código:
#include <stdio.h>
int main()
{
int numero1;
int numero2;
printf("Digite um valor para o primeiro numero: ");
scanf("%x",&numero1);
printf("Digite um valor para o segundo numero: ");
scanf("%x",&numero2);
printf("Valor 1 - Hexadecimal: %X, Decimal: %d\n",numero1,numero1);
printf("Valor 2 - Hexadecimal: %X, Decimal: %d\n",numero2,numero2);
return 0;
}O resultado no terminal será o seguinte, após os dois números inseridos pela pessoa usuária:
Desse modo, foi feita a conversão dos números digitados em hexadecimal para decimal. Vamos agora para as conversões!
Convertendo Hexadecimal para Decimal, Binário e Octal
Convertendo de Hexadecimal para Decimal
Vamos recapitular a tabela com os valores abaixo, pois, todos os cálculos que serão feitos, serão baseados nela:
Observação: Os números hexadecimais podem aparecer desse jeito: 5A16. É uma notação para informar que o número 5A está na base 16. Ou seja, ele é hexadecimal.
- Exemplo 1: Converter o número 5A, em hexadecimal, para decimal.
Para isso, todas as posições deverão ser elevadas em potências com o número 16. Nesse caso, o A está na posição 160, enquanto que o 5 está na posição 16¹. Vejamos o cálculo:
Qualquer número elevado a 0 é igual a 1. Ou seja, multiplicando 10×1 = 10. E, qualquer número elevado a 1 é igual a ele mesmo. Então, 5 x 16 = 80.
Como resultado, o número decimal é igual a 90.
- Exemplo 2: Converter o número 01A8 para decimal.
Mesmo procedimento:
Como resultado, o número decimal é igual a 424.
Convertendo de Decimal para Hexadecimal
Para isso, teremos que pegar os restos das divisões do número por 16 e, converter para hexadecimal:
- Exemplo 1: Converter o número 190 para hexadecimal.
Nesse caso, temos que dividir o número 190 por 16, até que o “resto” da divisão seja 0.
190/16 = 11 – resto 14
11/16 = 0 – resto 11
Como o número 11 que deixou a divisão zerada, ele que vem primeiro no hexadecimal.
O número 11 corresponderá a letra B e o número 14 a letra E, de acordo com a tabela.
Como resultado, o hexadecimal é igual a BE.
- Exemplo 2: Converter o número 1024 para hexadecimal.
Mesmo caso, pois devemos dividir o número 1024 por 16, até que o “resto” da divisão seja 0.
1024/16 = 64 – resto 0
64/16 = 4 – resto 0
4/16 = 0 – resto 4
Como o número 4 que deixou a divisão zerada, ele que vem primeiro no hexadecimal.
Como resultado, o hexadecimal é igual a 40016.
Convertendo de Hexadecimal para Binário
- Exemplo 1: transformar o número 9D8F, em binário.
9D8F – 1001 1101 1000 1111
- Exemplo 2: transformar o número F8AB em binário.
F8AB – 1111 1000 1010 1011
Convertendo de Binário para Hexadecimal
Para esse caso, devemos agrupar os dígitos binários de 4 em 4 e utilizar a tabela acima. Se for preciso, completar com zeros à esquerda.
- Exemplo 1: Transformar o número 11011010 em hexadecimal;
Separando:

O resultado será o número DA.
- Exemplo 2: Transformar o número 100011001000 em hexadecimal;
Separando:
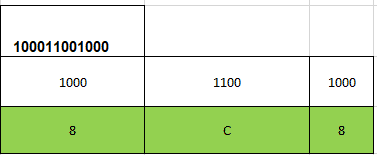
O resultado será o número 8C8.
Convertendo de Hexadecimal para Octal
Para valores octais, conforme foto abaixo, o processo é semelhante ao adotado para o sistema binário, mas representados com apenas três dígitos, ao invés de 4.
Para isso, vamos ao exemplo:
- Converter o hexadecimal BDD em octal.
Para isso, você deverá separar as três letras hexadecimais e convertê-las para os binários de cada uma. Depois disso, você junta o número inteiro em um binário e separa, desse binário gerado, grupos de 3 números. Feito isso, agora é necessário utilizar a tabela de octal acima, para chegar a resposta.
Ou seja, o hexadecimal BDD, em octal, será igual a 5735.
Convertendo de Octal para Hexadecimal
- Transformar o 57358 para hexadecimal.
Para o exemplo, vamos utilizar o mesmo octal do exemplo anterior. Quando um número tiver a notação 57358, por exemplo, você verá que ele terá a notação de base 8, representando a base octal.
Para essa conversão, será necessário você dividir o número octal de acordo com a tabela da base octal e juntar o resultado em um binário único. Feito isso, conforme o exemplo acima, você vai dividir o número binário em grupos de 4 números e verificar qual letra corresponde com o número gerado.
Para o exemplo, o número hexadecimal gerado será o BDD.
Quais as vantagens e desvantagens do sistema Hexadecimal?
A principal vantagem de utilização do hexadecimal é a redução do formato de seu número, se for comparado ao binário. Por exemplo:
- O número 1011 0110, em hexadecimal, ficaria B6 apenas.
- O número 0001 1011 1001 1010, em hexadecimal, ficaria 1B9A apenas.
Ou seja, à medida que os números ficam maiores, com hexadecimal, sua utilização e manuseio com operações fica mais simplificado. Além disso, pode causar uma economia muito grande de memória ou em seu servidor.
Já a desvantagem seria a de que, algumas pessoas podem ter dificuldades em utilizar esse sistema. Isso é uma coisa normal, pois você precisa ter um conhecimento básico do sistema binário antes de aprender sobre hexadecimais.
O hexadecimal é um número que possui dezesseis unidades, conforme você aprendeu e, dentre elas, estão dez números e seis letras.
Além disso, seu uso também é mais fácil, para possíveis conversões e operações. Uma de suas principais utilizações são para colorir as páginas web em sua aplicação.
Você quer mergulhar fundo nos sistemas de numeração? Então, não deixe de conferir o artigo sobre números binários!



